Question

Find the orthocenter of the triangle with the sides
\[
  x + y = 6 \\
  2x + y = 4 \\
  x + 2y = 5 \\
 \]

Answer 1

Hint: First, we have to find out the equation of altitudes as orthocenters are basically the intersection point of the three altitudes of the triangle. Since the equation of sides is given, we can find the equation of altitudes by finding the slope of the sides, and with the help of these equations of altitudes, we find the orthocenter by solving those equations.

Complete step by step answer:
 In \[\Delta ABC\], find the slope of lines using \[y = mx + c\] where \[m\] is the slope of a line
Let\[x + y = 6\]be the side AB whose slope is \[ - 1\]
$\Rightarrow$ \[2x + y = 4\], be the side BC with slope \[ - 2\]
$\Rightarrow$ \[x + 2y = 5\], be the side CA with slope \[ - \dfrac{1}{2}\]

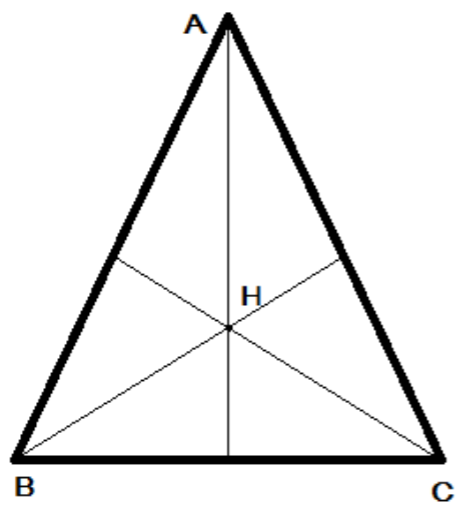
Then find the coordinates of vertices by solving the pair of side equations:
For Vertices A, solve line equation AB and CA by substitution method, we get A as:
 \[
\Rightarrow x + y = 6{\text{ or, }}x = 6 - y \\
\Rightarrow x + 2y = 5 \\
\Rightarrow 6 - y + 2y = 5 \\
\Rightarrow y = - 1 \\
\Rightarrow x = 6 - ( - 1) = 7 \\
\Rightarrow \left( {{A_X},{A_Y}} \right) \equiv (7, - 1) \\
 \]

For Vertices B, solve equation AB and BC by substitution method, we get:
\[
\Rightarrow x + y = 6{\text{ or, }}x = 6 - y \\
\Rightarrow 2x + y = 4{\text{ or, }}2(6 - y) + y = 4 \\
\Rightarrow 12 - 2y + y = 4 \\
\Rightarrow y = 12 - 4 = 8 \\
\Rightarrow x = 6 - y = 6 - 8 = - 2 \\
\Rightarrow \left( {{B_X},{B_Y}} \right) \equiv ( - 2,8) \\
 \]

For Vertices C, solve equation BC and CA by substitution method, we get:
\[
\Rightarrow x + 2y = 5{\text{ or, }}x = 5 - 2y \\
\Rightarrow 2x + y = 4{\text{ or, }}2(5 - 2y) + y = 4 \\
\Rightarrow 10 - 4y + y = 4 \\
\Rightarrow 3y = 6 \\
\Rightarrow y = 2 \\
\Rightarrow x = 5 - 2y = 5 - 2(2) = 1 \\
\Rightarrow \left( {{C_X},{C_Y}} \right) \equiv (1,2) \\
 \]

So, we have all the vertices of the triangle as:
\[
\Rightarrow \left( {{A_X},{A_Y}} \right) \equiv (7, - 1) \\
\Rightarrow \left( {{B_X},{B_Y}} \right) \equiv ( - 2,8) \\
\Rightarrow \left( {{C_X},{C_Y}} \right) \equiv (1,2) \\
 \]

Now, find the altitude AD, BE, CF of the \[\Delta ABC\] by using the slope and equation of opposite vertex.
So, the equation for AD will be given as:
\[
\Rightarrow \dfrac{{y - {A_y}}}{{x - {A_x}}} = \dfrac{{ - 1}}{{slope\left( {BC} \right)}} \\
\Rightarrow \dfrac{{y + 1}}{{x - 7}} = \dfrac{1}{2} \\
\Rightarrow x - 7 = 2(y + 1) \\
\Rightarrow x - 7 = 2y + 2 \\
\Rightarrow x - 2y - 9 = 0 \\
 \]
By cross multiplying the terms, we get:
\Rightarrow \[x - 2y - 9 = 0\]-- (i)

Again, the equation for BE will be
 \[
\Rightarrow \dfrac{{y - {B_y}}}{{x - {B_x}}} = \dfrac{{ - 1}}{{slope\left( {CA} \right)}} \\
\Rightarrow \dfrac{{y - 8}}{{x + 2}} = 2 \\
\Rightarrow 2(x + 2) = y - 8 \\
\Rightarrow 2x + 4 = y - 8 \\
\Rightarrow 2x - y = - 12 \\
\Rightarrow 2x - y + 12 = 0 \\
 \]
By cross multiplying the terms, we get:
\Rightarrow\[2x - y + 12 = 0\]-- (ii)

Similarly, the equation for CF will be
\[
\Rightarrow \dfrac{{y - {C_y}}}{{x - {C_x}}} = \dfrac{{ - 1}}{{slope\left( {AB} \right)}} \\
\Rightarrow \dfrac{{y - 2}}{{x - 1}} = 1 \\
 \]
By cross multiplying the terms, we get:
\[
\Rightarrow x - 1 = y - 2 \\
\Rightarrow x - y + 1 = 0 \\
\Rightarrow x = y - 1 - - - (iii) \\
 \]
Then find the orthocenter we can find by solving any two equations of the altitude (i), (ii), (iii):
Substitute $x = y - 1$ in the equation \[x - 2y + 9 = 0\] to determine the value of the variables $\left( {x,y} \right)$.
$
\Rightarrow x - 2y - 9 = 0 \\
\Rightarrow y - 1 - 2y - 9 = 0 \\
\Rightarrow - y - 10 = 0 \\
\Rightarrow y = - 10 \\
 $
Again, substitute $y = - 10$ in the equation $x = y - 1$ to determine the value of $y$.
$
\Rightarrow x = y - 1 \\
\Rightarrow x = - 10 - 1 \\
\Rightarrow x = - 11 \\
 $
Hence, we get \[H\left( { - 11, - 10} \right)\] as an orthocenter.

Note: Orthocenters are always the intersection point of altitudes so first find the equation of altitudes. Altitudes are the perpendicular line segment drawn from any one of the vertices of the triangle to any one of the sides of the triangle.