Question

Find the parametric equation of the part of circle (lying in the quadrant IV) for the circle ${{x}^{2}}+{{y}^{2}}-2x+4y-4=0$.

Answer 1

Hint: The parametric equation of a circle can be written as $\begin{align}
  & x=r\cos t+{{x}_{0}} \\
 & y=r\sin t+{{y}_{0}} \\
\end{align}$, where $r$ is the radius of the circle and $({{x}_{0}},{{y}_{0}})$ is the centre of the circle. However, there are some restrictions on the $x$ and $y$ coordinate in this question, and keep those restrictions in mind while solving the questions, because you’ll get bounds on $t$ by imposing those restrictions.
The parametric equation of a circle can be written as $\begin{align}
  & x=r\cos t+{{x}_{0}} \\
 & y=r\sin t+{{y}_{0}} \\
\end{align}$, where $r$ is the radius of the circle and $({{x}_{0}},{{y}_{0}})$ is the centre of the circle. However, there are some restrictions on the $x$ and $y$ coordinate in this question, and keep those restrictions in mind while solving the questions, because you’ll get bounds on $t$ by imposing those restrictions.
Generalising first, the parametric equation of any circle with a general equation ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$, with a centre $C$ = $(-g,-f)$, and radius $r$=$\sqrt{{{g}^{2}}+{{f}^{2}}-c}$, is :
$\begin{align}
  & x=r\cos t+g \\
 & y=r\sin t+f \\
\end{align}$ ……………………….(1)
Where $t$ is the angle the point in consideration makes with the positive $x$ axis.
The equation of the circle given to us is : ${{x}^{2}}+{{y}^{2}}-2x+4y-4=0$
Comparing it with the general equation of a circle, we get :
$\begin{align}
  & 2gx=-2x \\
 & \Rightarrow 2g=-2 \\
 & \Rightarrow g=-1 \\
\end{align}$ and $\begin{align}
  & 2fy=+4y \\
 & \Rightarrow 2f=4 \\
 & \Rightarrow f=2 \\
\end{align}$
Hence, the centre of the circle mentioned $C$ = $(-g,-f)=(1,-2)$
And its radius $r$ = $\sqrt{{{g}^{2}}+{{f}^{2}}-c}=\sqrt{{{1}^{2}}+{{2}^{2}}+4}=\sqrt{9}=3$
Plugging these values into equation (1), we get :
$\begin{align}
  & x=3\cos t-1 \\
 & y=3\sin t+2 \\
\end{align}$ …………………(2)
However, in the question, we have a restriction to be followed on the values of $x$ and $y$. It says that the point on the circle should be lying on the fourth quadrant only. This means that the $x$ coordinate of the point has to be positive, and the $y$ coordinate has to be negative.
Here’s a figure representing the circle on a graph :

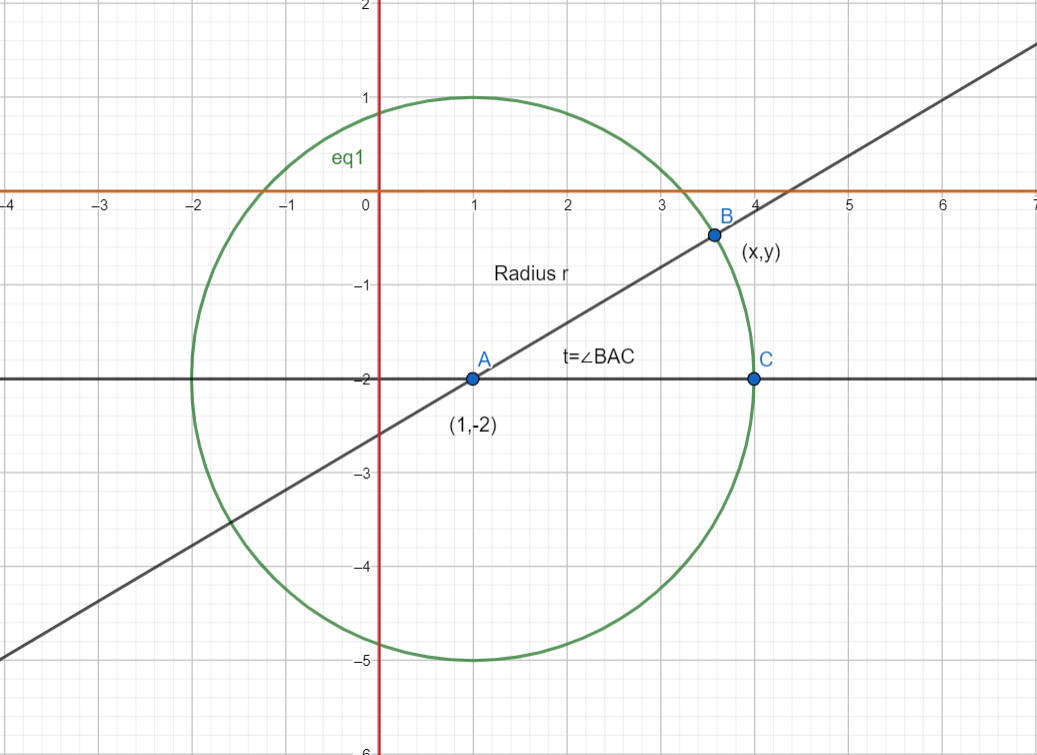
The $x$ and $y$ axes are highlighted and it should be noted that the points required should only lie in the region where $y$ is negative and $x$ is positive, as we can see.
Applying these conditions to the set of equations (2), we’ll have :
$\begin{align}
  & x>0 \\
 & \Rightarrow 3\cos t-1>0 \\
 & \Rightarrow 3\cos t>1 \\
 & \Rightarrow \cos t>\dfrac{1}{3} \\
 & \Rightarrow t\in (-{{\cos }^{-1}}\dfrac{1}{3},{{\cos }^{-1}}\dfrac{1}{3}) \\
\end{align}$ and $\begin{align}
  & y<0 \\
 & \Rightarrow 3\sin t+2<0 \\
 & \Rightarrow 3\sin t<-2 \\
 & \Rightarrow \sin t<-\dfrac{2}{3} \\
 & \Rightarrow t\in (-{{\sin }^{-1}}\dfrac{2}{3},\pi +{{\sin }^{-1}}\dfrac{2}{3}) \\
\end{align}$
Combining the two conditions on $t$, we get the final condition as :
$t\in (-{{\sin }^{-1}}\dfrac{2}{3},{{\cos }^{-1}}\dfrac{1}{3})$
 $
   x=3\cos t-1 \\
  y=3\sin t+2 \\
$ , $t\subset (-{{\sin }^{-1}}\dfrac{2}{3},{{\cos }^{-1}}\dfrac{1}{3})$

Note: It is important that the condition on t be mentioned, since, if this condition is not imposed, then the parametric equations will be valid for every point on the circle, but we have been asked to find points lying only in the fourth quadrant, and hence, the condition on $t$ is necessary.