Question

Find the perimeter of a triangle with sides $3{\text{ cm, }}8{\text{ cm}}$ and $6{\text{ cm}}$.

Answer 1

Hint: The perimeter of a plane surface is the length of its boundaries. Thus, the perimeter of a triangle is the sum of all of its sides. Add the given sides of the triangle to determine its perimeter.

Complete step-by-step answer:
According to the given question, the sides of the triangle are $3{\text{ cm, }}8{\text{ cm}}$ and $6{\text{ cm}}$.

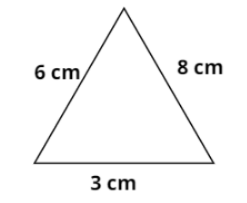
We know that the perimeter of a plane surface is the length of its boundaries.
But since a triangle consists of three sides, its perimeter will be the sum of all of its sides. Therefore using this we will get the perimeter as:
$ \Rightarrow $ Perimeter \[ = 3{\text{ cm }} + 8{\text{ cm }} + {\text{ }}6{\text{ cm}} = 17{\text{ cm}}\]

Thus the perimeter of the triangle is 17 cm.

Additional Information:
If the area of the triangle is asked instead, then we can use the formula:
\[ \Rightarrow {\text{ Area}} = \dfrac{1}{2} \times b \times h\], where $b$ is the base and $h$ is the height of the triangle.
If all the sides of the triangle are known then Heron’s formula can also be used to determine its area. This formula is:
\[ \Rightarrow {\text{ Area}} = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} \], where \[a,{\text{ }}b\] and $c$ are the sides of the triangle and $s$ is the semi-perimeter. So the value of $s$ is $s = \dfrac{{a + b + c}}{2}$.
If the triangle is a right angled triangle instead, then its area can be calculated by the formula:
\[ \Rightarrow {\text{ Area}} = \dfrac{1}{2} \times {\text{base}} \times {\text{perpendicular}}\]

Note: For three lines to form a triangle, the sum of the lengths of any two of them must be greater than the length of the third one. In the above question, the lengths of the sides of the triangle are $3{\text{ cm, }}8{\text{ cm}}$ and $6{\text{ cm}}$ and we can see that:
\[ \Rightarrow 3 + 8 > 6,{\text{ }}3 + 6 > 8\] and $8 + 6 > 3$
Therefore the condition is valid for a triangle.