
Find the quadrant or axis in/on which the following point lies
A. I
B. II
C. III
D. None of these
Answer
384.9k+ views
Hint: Here, we are given a point and we need to find out in which quadrant it lies. Also, one should note that the x coordinate is always written first and the y coordinate is written next. And so, starting from the top right corner is Quadrant I and then, in a counter clockwise direction you will see Quadrants II, III and IV. Thus, we will notice the sign of the coordinates in each point and then compare them with the standard form of the quadrants to get the final output.
Complete step by step answer:
Given, one point
We know that, when we draw a horizontal line and then a vertical line, both intersect and that intersection point is called the origin. Then, from the reference of origin and those two lines we define quadrants, the horizontal line is called x-axis and the vertical line is called y-axis and so we get 4 quadrants in all.
For this, we will first understand the type of points every quadrant has and then compare them with the given point to find the required quadrant in which the given point lies.
So, we have drawn the figure below:
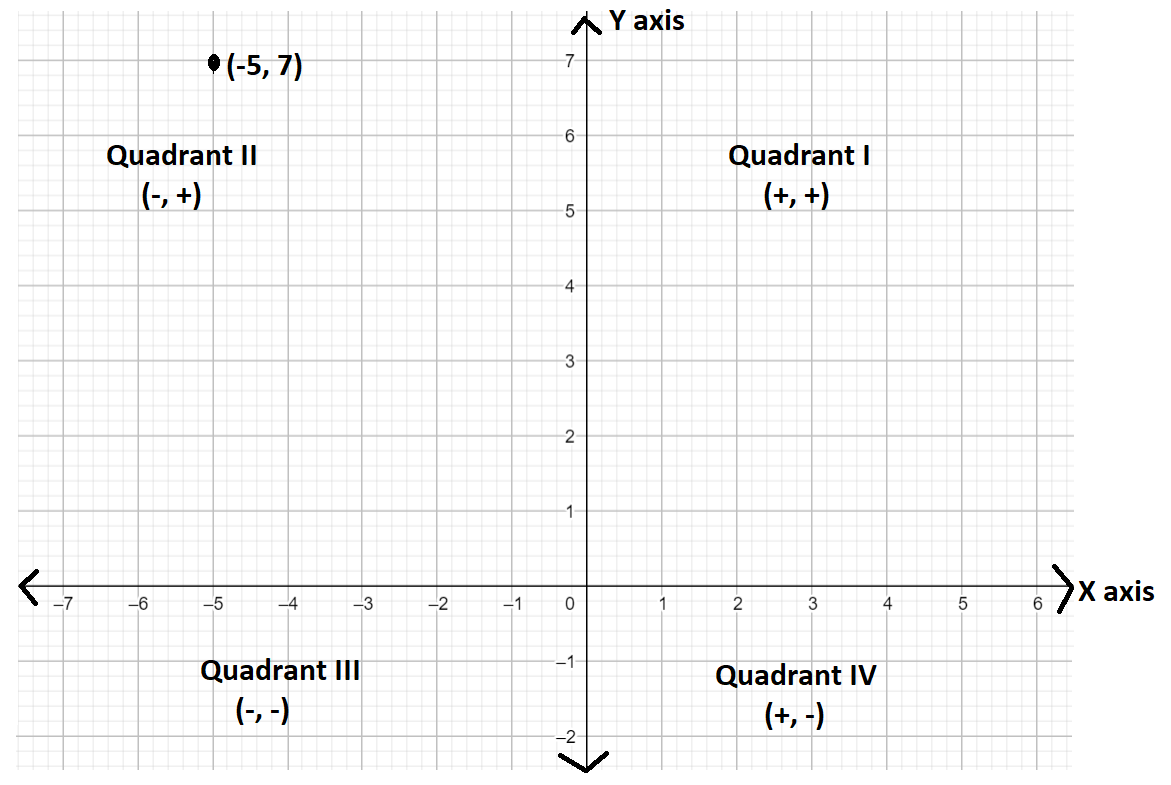
According to the figure, both the coordinates are there in all the 4 quadrants as shown below:
1) 1st quadrant: x is positive and y is positive
2) 2nd quadrant: x is negative and y is positive
3) 3rd quadrant: x is negative and y is negative
4) 4th quadrant: x is positive and y is negative.
We are given a point
So, from the figure, we can say that this point is in the 2nd quadrant.
Hence, the point
Note:
A quadrant is the area contained by the x and y axis. To explain this, the two dimensional Cartesian plane is divided by the x and y axis into four quadrants. Students often make mistakes in naming quadrants in the Cartesian plane. Also remember, the quadrant starts from the top right corner and moves in an anticlockwise direction.
Complete step by step answer:
Given, one point
We know that, when we draw a horizontal line and then a vertical line, both intersect and that intersection point is called the origin. Then, from the reference of origin and those two lines we define quadrants, the horizontal line is called x-axis and the vertical line is called y-axis and so we get 4 quadrants in all.
For this, we will first understand the type of points every quadrant has and then compare them with the given point to find the required quadrant in which the given point lies.
So, we have drawn the figure below:

According to the figure, both the coordinates are there in all the 4 quadrants as shown below:
1) 1st quadrant: x is positive and y is positive
2) 2nd quadrant: x is negative and y is positive
3) 3rd quadrant: x is negative and y is negative
4) 4th quadrant: x is positive and y is negative.
We are given a point
So, from the figure, we can say that this point is in the 2nd quadrant.
Hence, the point
Note:
A quadrant is the area contained by the x and y axis. To explain this, the two dimensional Cartesian plane is divided by the x and y axis into four quadrants. Students often make mistakes in naming quadrants in the Cartesian plane. Also remember, the quadrant starts from the top right corner and moves in an anticlockwise direction.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

Why is steel more elastic than rubber class 11 physics CBSE

Explain why a There is no atmosphere on the moon b class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE




