
Find the ratio in which the point (- 3, p) divides the line segment joining the points (-5, -4) and (-2, 3). Hence, find the value of p.
Answer
501k+ views
Hint: In this question to find the values of p, we will assume that the point (-3, p) divides the line joining the points (-5, -4) and (-2, 3) in the ratio of k : 1. And will use the section formula to find the value of p and k.
Complete step-by-step solution -
Now, we will use the section formula. The section formula tells us the coordinates of a point which divides a given line segment into two parts such that their lengths are in the ratio m: n. The Section formula to find a point (x, y) is
x = $\dfrac{{{\text{m}}{{\text{x}}_2}{\text{ + n}}{{\text{x}}_1}}}{{{\text{m + n}}}}$
y = $\dfrac{{{\text{m}}{{\text{y}}_2}{\text{ + n}}{{\text{y}}_1}}}{{{\text{m + n}}}}$
Here we are given two points. Let say A (-5, -4) and B (-2, 3) makes a line segment AB. The line segment AB is divided at point Q, so, we will apply section formula at point Q.
Let Q (-3, p) divide the line segment AB in the ratio k : 1.
So, applying section formula at point Q (-3, p), we get
x – coordinate of Q = $\dfrac{{k\left( { - 2} \right) + 1\left( { - 5} \right)}}{{k + 1}}$ = $\dfrac{{ - 2k - 5}}{{k + 1}}$
y – coordinate of Q = $\dfrac{{k\left( 3 \right) + 1\left( { - 4} \right)}}{{k + 1}} = \dfrac{{3k - 4}}{{k + 1}}$
Now as we know that the coordinates of point Q is (-3, p)
So, on comparing the x – coordinate of point Q. We get,
$\dfrac{{ - 2k - 5}}{{k + 1}} = - 3$
Cross-multiplying above equation to find the value of k. We get,
– 2k – 5 = – 3(k + 1)
– 2k – 5 = – 3k – 3
Adding 3k + 5 to both the sides of the above equation. We get,
k = 2
Now to find the value of p we had to compare the y -coordinate of point Q with p and put the value of k = 2.
So, p = $\dfrac{{3k - 4}}{{k + 1}}$
Now putting the value of k as 2 in the RHS of the above equation. We get,
p = $\dfrac{{3\left( 2 \right) - 4}}{{2 + 1}} = \dfrac{2}{3}$
Hence, the point $\left( { - 3,\dfrac{2}{3}} \right)$ divides the line segment joining the points (-5, -4) and (-2, 3) in ratio 2 : 1.
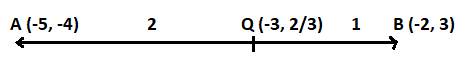
Note: While solving such types of questions, it is important to apply the section formula correctly. Most of the students made a mistake while applying the section formula. They replaced m from n and n from m. Also, apply the proper ratio for finding the coordinates of a point. Also, when only you have to find the value of a given variable, apply only that formula to find the value of the variable, for example if you are given that the x – coordinate of point is k, so you have to apply only the formula to find the x – coordinate of point.
Complete step-by-step solution -
Now, we will use the section formula. The section formula tells us the coordinates of a point which divides a given line segment into two parts such that their lengths are in the ratio m: n. The Section formula to find a point (x, y) is
x = $\dfrac{{{\text{m}}{{\text{x}}_2}{\text{ + n}}{{\text{x}}_1}}}{{{\text{m + n}}}}$
y = $\dfrac{{{\text{m}}{{\text{y}}_2}{\text{ + n}}{{\text{y}}_1}}}{{{\text{m + n}}}}$
Here we are given two points. Let say A (-5, -4) and B (-2, 3) makes a line segment AB. The line segment AB is divided at point Q, so, we will apply section formula at point Q.
Let Q (-3, p) divide the line segment AB in the ratio k : 1.
So, applying section formula at point Q (-3, p), we get
x – coordinate of Q = $\dfrac{{k\left( { - 2} \right) + 1\left( { - 5} \right)}}{{k + 1}}$ = $\dfrac{{ - 2k - 5}}{{k + 1}}$
y – coordinate of Q = $\dfrac{{k\left( 3 \right) + 1\left( { - 4} \right)}}{{k + 1}} = \dfrac{{3k - 4}}{{k + 1}}$
Now as we know that the coordinates of point Q is (-3, p)
So, on comparing the x – coordinate of point Q. We get,
$\dfrac{{ - 2k - 5}}{{k + 1}} = - 3$
Cross-multiplying above equation to find the value of k. We get,
– 2k – 5 = – 3(k + 1)
– 2k – 5 = – 3k – 3
Adding 3k + 5 to both the sides of the above equation. We get,
k = 2
Now to find the value of p we had to compare the y -coordinate of point Q with p and put the value of k = 2.
So, p = $\dfrac{{3k - 4}}{{k + 1}}$
Now putting the value of k as 2 in the RHS of the above equation. We get,
p = $\dfrac{{3\left( 2 \right) - 4}}{{2 + 1}} = \dfrac{2}{3}$
Hence, the point $\left( { - 3,\dfrac{2}{3}} \right)$ divides the line segment joining the points (-5, -4) and (-2, 3) in ratio 2 : 1.
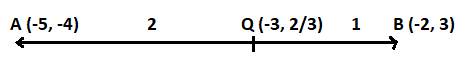
Note: While solving such types of questions, it is important to apply the section formula correctly. Most of the students made a mistake while applying the section formula. They replaced m from n and n from m. Also, apply the proper ratio for finding the coordinates of a point. Also, when only you have to find the value of a given variable, apply only that formula to find the value of the variable, for example if you are given that the x – coordinate of point is k, so you have to apply only the formula to find the x – coordinate of point.
Recently Updated Pages
The correct geometry and hybridization for XeF4 are class 11 chemistry CBSE

Water softening by Clarks process uses ACalcium bicarbonate class 11 chemistry CBSE

With reference to graphite and diamond which of the class 11 chemistry CBSE

A certain household has consumed 250 units of energy class 11 physics CBSE

The lightest metal known is A beryllium B lithium C class 11 chemistry CBSE

What is the formula mass of the iodine molecule class 11 chemistry CBSE

Trending doubts
The reservoir of dam is called Govind Sagar A Jayakwadi class 11 social science CBSE

10 examples of friction in our daily life

What problem did Carter face when he reached the mummy class 11 english CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

State and prove Bernoullis theorem class 11 physics CBSE

Proton was discovered by A Thomson B Rutherford C Chadwick class 11 chemistry CBSE




