
Find the ratio in which the point
Answer
500.7k+ views
Hint: We will first start defining the section formula and then we will apply the section formula for internal division that is
Complete step by step answer:
To find the ratio in which the point
So basically, the section formula tells us the coordinates of the point which divides a given line segment into two parts such that their lengths are in the ratio
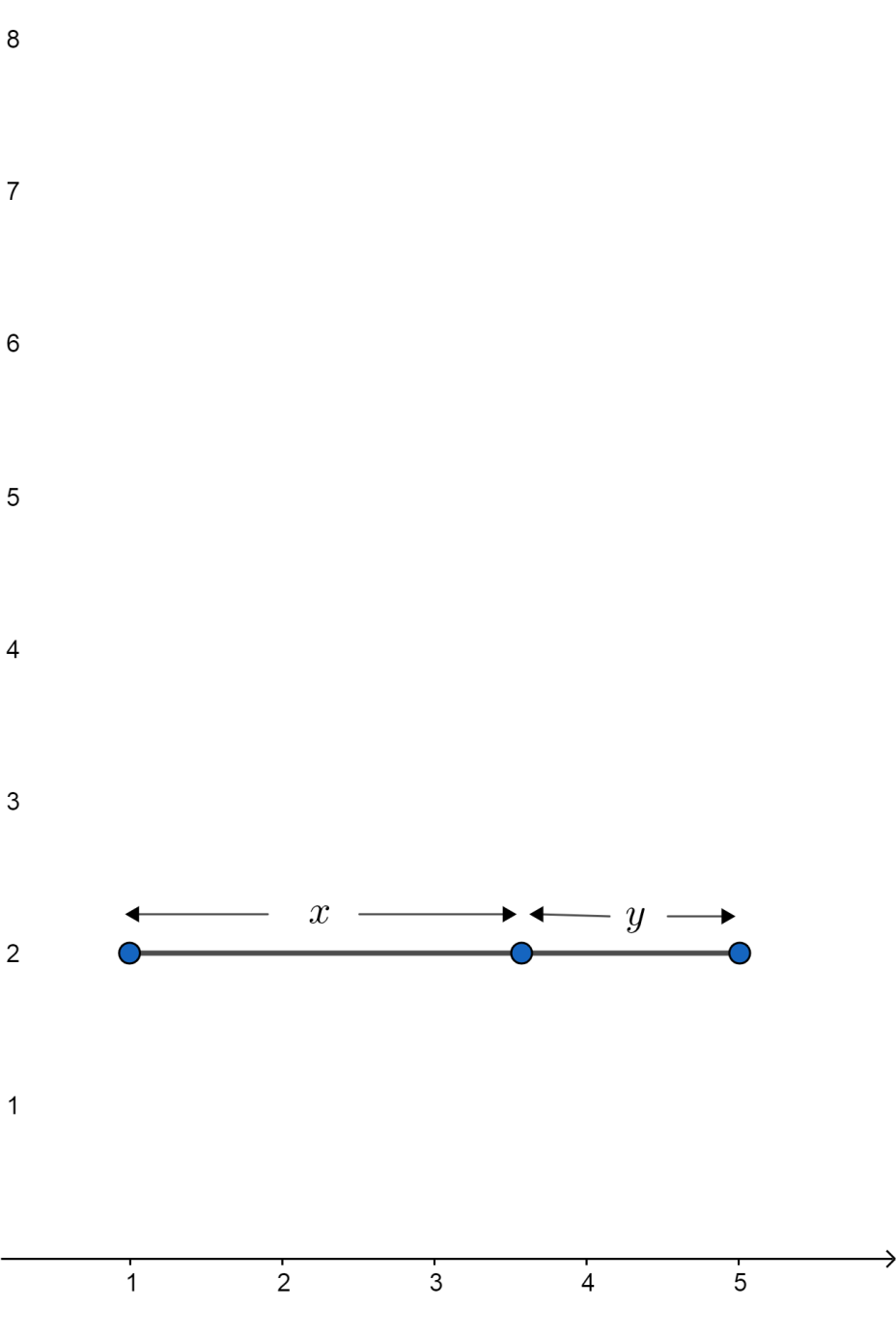
Now, let’s see the formula of the internal division with section formula:
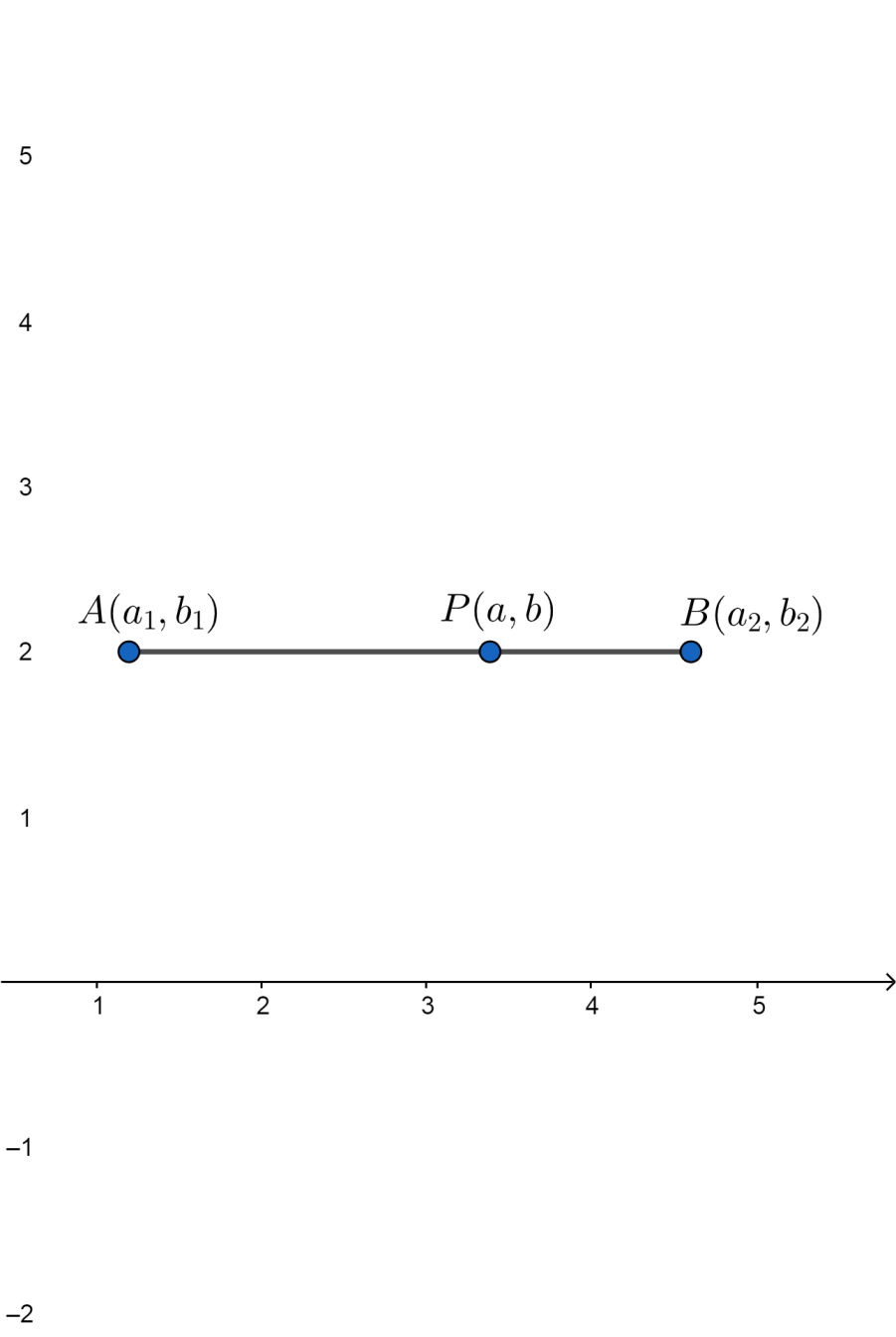
If point
So, let’s take the question, and see it is given that the point
Now, we can solve this question in normal method by assuming the ratio to be
Now the required ratio will be
Now we have
Therefore, the ratio in which
Note:
We can also solve this by following method with the graph, so we have:
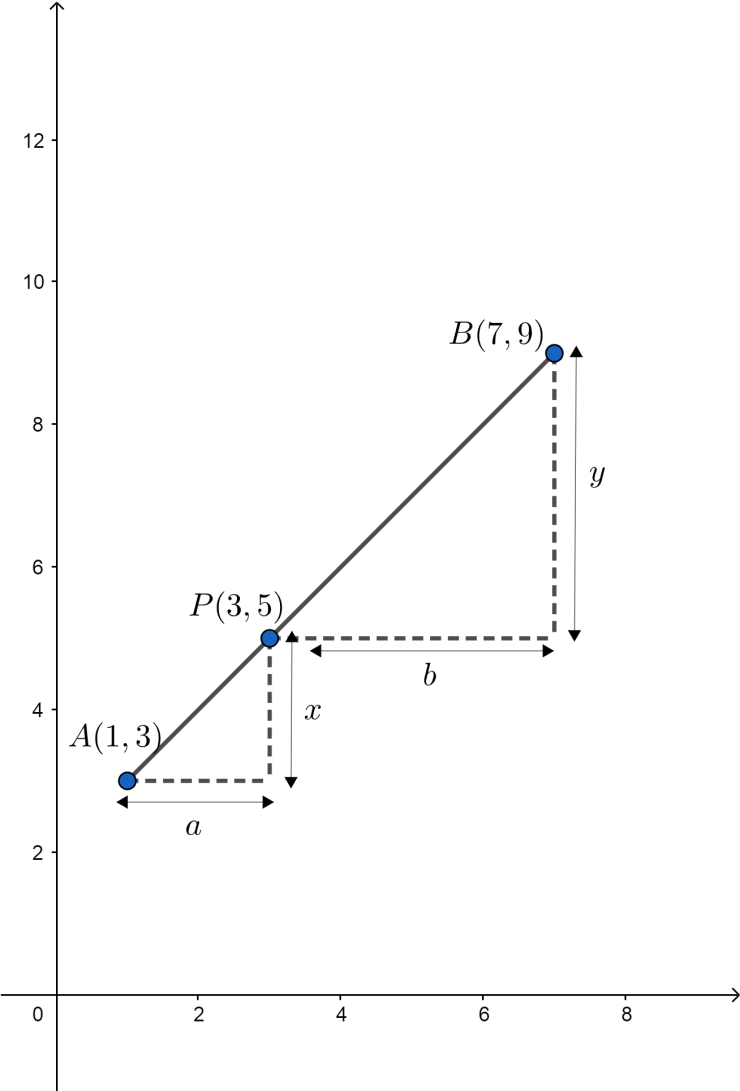
Now, from the graph we have:
Therefore, the ratio is
Complete step by step answer:
To find the ratio in which the point
So basically, the section formula tells us the coordinates of the point which divides a given line segment into two parts such that their lengths are in the ratio

Now, let’s see the formula of the internal division with section formula:

If point
So, let’s take the question, and see it is given that the point
Now, we can solve this question in normal method by assuming the ratio to be
Now the required ratio will be
Now we have
Therefore, the ratio in which
Note:
We can also solve this by following method with the graph, so we have:

Now, from the graph we have:
Therefore, the ratio is
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the full form of POSCO class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

Fill the blanks with proper collective nouns 1 A of class 10 english CBSE




