Question

Find the ratio in which the y-axis divides the line segment joining the points (5,-6) and (-1,-4). Also, find the coordinates of the point of division.

Answer 1

Hint: In this question, we will use the concept of section formulae of coordinate geometry. This states that the coordinate of the point which divides the line segment joining the points $({x_1},{y_1})$and $({x_2},{y_2})$ internally in the ratio m:n is given by $\left( {x = \dfrac{{m{x_2} + n{x_1}}}{{m + n}},y = \dfrac{{m{y_2} + n{y_1}}}{{m + n}}} \right)$. …….(i)

Complete step-by-step answer:
Here , we have given points of the line segment , (5,-6) and (-1,-4)
Comparing this with $({x_1},{y_1})$and $({x_2},{y_2})$, we get
${x_1} = 5,{x_2} = - 1,{y_1} = - 6$ and ${y_2} = - 4$.
Let the required ratio be k:1.
Then by using the section formula,
$\left( {x = \dfrac{{m{x_2} + n{x_1}}}{{m + n}},y = \dfrac{{m{y_2} + n{y_1}}}{{m + n}}} \right)$
According to the question, the point of division is on the y-axis, hence the x- coordinate of that point is 0.
Then, the coordinates of the point of division are,
$
   \Rightarrow x = \dfrac{{m{x_2} + n{x_1}}}{{m + n}} \\
   \Rightarrow 0 = \dfrac{{k( - 1) + 1(5)}}{{k + 1}} \\
   \Rightarrow 0 = 5 - k \\
   \Rightarrow k = 5 \\
$
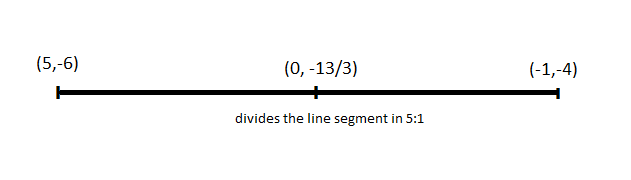
Hence, the ratio in which the y-axis divides the line segment is 5:1.
Now we have to find the coordinates of the point of division on y-axis, i.e. (0,y)
$ \Rightarrow $$y = \dfrac{{m{y_2} + n{y_1}}}{{m + n}}$
$
   \Rightarrow y = \dfrac{{5( - 4) + 1( - 6)}}{{5 + 1}} \\
   \Rightarrow y = \dfrac{{ - 20 - 6}}{6} = \dfrac{{ - 26}}{6} \\
   \Rightarrow y = \dfrac{{ - 13}}{3} \\
$
Hence, the coordinates of the point of division is $\left( {0,\dfrac{{ - 13}}{3}} \right)$.

Note: In this type of question we have to remember the concept of the section formulae .First we have to find out the required values and then we will assume that the line segment will be divided in k:1. After that we will find out the coordinates of the point of division by putting those values in section formulae i.e. $\left( {x = \dfrac{{m{x_2} + n{x_1}}}{{m + n}},y = \dfrac{{m{y_2} + n{y_1}}}{{m + n}}} \right)$. After solving the formula step by step, we will get the required ratio of division and the coordinates of point of division.