Question

Find the reading of the spring balance shown in the figure. The elevator is going up with an acceleration of $g/10$, the pulley and the string are light and the pulley is smooth.

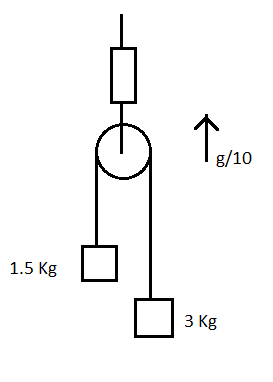
Answer 1

Hint: This problem can be easily solved in the frame of reference of the elevator. Since the elevator and hence, the frame of reference moves up with an acceleration of $g/10$, all the bodies in this frame will have a downward pseudo force of $mg/10$ where $m$is the mass of the body. The tension in the pulley will be twice that in the string since the string is pulling down on the pulley from both sides.
Formula used:
$F=ma$
Where $F$ is the force exerted on or by a body, $m$ is the mass of the body and $a$ is the acceleration of the body in the direction of the force.

Complete step by step answer:
We can solve this problem in the non-inertial frame of reference of the elevator. Now, when we are solving in a non-inertial frame of reference which is accelerating, a pseudo force must be applied on all bodies of the frame such that the pseudo force produces an acceleration on all bodies in the opposite direction as that of the acceleration of the frame of reference.
Thus, in this problem we will consider the frame of reference of the elevator. Thus, the frame of reference moves upward with an acceleration of $g/10$. Hence, all the bodies in this frame of reference will have a pseudo force $mg/10$ in the downward direction, where $m$ is the mass of the body.

Now, since the string over the pulley is inextensible, it will have the same uniform magnitude of acceleration throughout. Thus, if the mass $3Kg$ moves down by acceleration $a$, the mass $1.5Kg$ will move up by the same acceleration $a$.
Let the tension in the string in the pulley be $T$.

Now we will draw the free body diagrams of the $1.5Kg$ block.

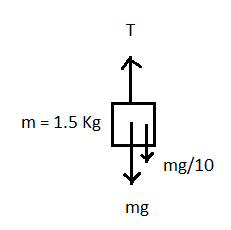
Where $m=1.5Kg$ is the mass of the block, $mg$ is its weight, $mg/10$ is the pseudo force on the block and $T$ is the tension from the rope on the block.

Now we will draw the free body diagrams of the $3Kg$ block.

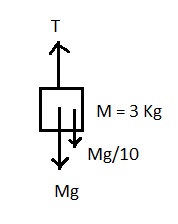
Where $M=3Kg$ is the mass of the block, $Mg$ is its weight, $Mg/10$ is the pseudo force on the block and $T$ is the tension from the rope on the block.
Hence, using this information, let us apply, in the vertical axis,

$F=ma$--(1)

Where $F$ is the force exerted on or by a body, $m$ is the mass of the body and $a$ is the acceleration of the body in the direction of the force.

Therefore, as explained above let the $1.5Kg$ block go up with an acceleration $a$ and the $3Kg$ block go down with an acceleration $a$.

Hence, using (1), for the $1.5Kg$ block, we get,

$T-mg-mg/10=ma$ (assigning proper signs to the magnitudes depending on their direction and considering the upward direction to be positive)
$\therefore T-\dfrac{11mg}{10}=ma$
$\therefore a=\dfrac{T}{m}-\dfrac{11g}{10}=\dfrac{T}{1.5}-\dfrac{11g}{10}$ --(2) $\left( \because m=1.5Kg \right)$

Now, , using (1), for the $3Kg$ block, we get,

$Mg+Mg/10-T=Ma$ (assigning proper signs to the magnitudes depending on their direction and considering the upward direction to be positive)

$\therefore \dfrac{11Mg}{10}-T=Ma$
$\therefore a=\dfrac{11g}{10}-\dfrac{T}{M}=\dfrac{11g}{10}-\dfrac{T}{3}$ --(3) $\left( \because M=3Kg \right)$

Hence, now equating (2) and (3), we get,

$\dfrac{T}{1.5}-\dfrac{11g}{10}=\dfrac{11g}{10}-\dfrac{T}{3}$
$\therefore \dfrac{T}{1.5}+\dfrac{T}{3}=\dfrac{11g}{10}+\dfrac{11g}{10}$
$\therefore \dfrac{2T+T}{3}=\dfrac{22g}{10}$
$\therefore \dfrac{3T}{3}=\dfrac{22g}{10}$
$\therefore T=\dfrac{22g}{10}$
Hence, the tension in the string is $\dfrac{22g}{10}$

Now since, the string pulls on the pulley downward from both sides the tension in the string joining the spring balance and the pulley pulls the pulley upward with double the tension of the string on the pulley, that is, by $2T$. Thus this tension also causes the reading of the spring balance.

The reading of the spring balance is the pulling force on it divided by the acceleration due to gravity $g$.
Hence, the reading of the spring balance will be,

$\dfrac{2T}{g}=\dfrac{\dfrac{2\times 22g}{10}}{g}=\dfrac{22}{5}=4.4Kg$

Note: Sometimes solving a problem in a non-inertial frame of reference takes care of many unknown variables and makes the problem easier. However, students must keep in mind that proper pseudo forces should be assigned before starting to solve a problem in a non-inertial frame of reference. The direction of the pseudo forces have to be especially taken care of. Often students make the mistake of giving the pseudo force the same direction as that of the acceleration of the frame of reference. However, the absolute opposite must be done.
Pseudo forces only have to be applied when the non-inertial frame of reference is accelerating. If the frame of reference is moving with a constant velocity, no pseudo forces act on the bodies in the frame. Drawing proper free body diagrams is of prime importance in solving mechanics problems. Proper free body diagrams break complex problems into simpler parts and make it easier. The habit of drawing proper free body diagrams must be thoroughly practiced by a student.