Question

Find the set of all real values of x for which $\dfrac{{8{x^2} + 16x - 51}}{{(2x - 3)(x + 4)}} < 3$.
A) $( - 3,\dfrac{5}{2})$
B) $( - 4, - 3)$
C) Both A and B
D) None of these

Answer 1

Hint: we will simplify the inequality and then find the values of the ‘x’ satisfying the inequality by plotting the equation.
Given,
$\dfrac{{8{x^2} + 16x - 51}}{{(2x - 3)(x + 4)}} < 3 \to (1)$
Now, let us simplify the inequality by adding -3 on both sides of equation (1), we get
$
   \Rightarrow \dfrac{{8{x^2} + 16x - 51}}{{(2x - 3)(x + 4)}} - 3 < 3 - 3 \\
   \Rightarrow \dfrac{{8{x^2} + 16x - 51}}{{(2x - 3)(x + 4)}} - 3 < 0 \\
   \Rightarrow \dfrac{{8{x^2} + 16x - 51 - (3(2x - 3)(x + 4))}}{{(2x - 3)(x + 4)}} < 0 \\
$
Now, solving the numerator, we get
$
   \Rightarrow \dfrac{{8{x^2} + 16x - 51 - (3(2{x^2} + 5x - 12))}}{{(2x - 3)(x + 4)}} < 0 \\
   \Rightarrow \dfrac{{8{x^2} + 16x - 51 - 6{x^2} - 15x + 36}}{{(2x - 3)(x + 4)}} < 0 \\
   \Rightarrow \dfrac{{2{x^2} + x - 15}}{{(2x - 3)(x + 4)}} < 0 \to (2) \\
$
Now, multiply and divide the L.H.S of equation (2) with $'(2x - 3)(x + 4)'$ , we get
$
   \Rightarrow \dfrac{{2{x^2} + x - 15}}{{(2x - 3)(x + 4)}}*(\dfrac{{(2x - 3)(x + 4)}}{{(2x - 3)(x + 4)}}) < 0 \\
   \Rightarrow \dfrac{{(2{x^2} + x - 15)((2x - 3)(x + 4))}}{{{{((2x - 3)(x + 4))}^2}}} < 0 \to (3) \\
$
Now, factoring the quadratic equation $2{x^2} + x - 15$ we get $(2x - 5)(x + 3)$ .Therefore, rewriting the equation (3), we get
$ \Rightarrow \dfrac{{(2x - 5)(x + 3)((2x - 3)(x + 4))}}{{{{((2x - 3)(x + 4))}^2}}} < 0 \to (4)$
Now, we can say the denominator is positive, since the square is always positive.
Now, to find the values of x we will only numerator i.e..,
$(2x - 5)(x + 3)((2x - 3)(x + 4)) < 0$
Solving the inequality by plotting, we get

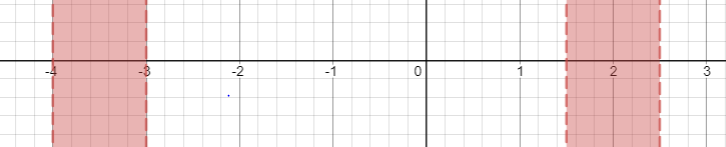
Hence, when $x \in ( - 4, - 3) \cup (\dfrac{3}{2},\dfrac{5}{2})$ , equation (4) will be negative.
So, from the options given, only ‘B’ is suitable. Hence, option ‘B’ i.e.., $( - 4, - 3)$ is the required solution.
Note: Since, the denominator value is positive, therefore we have considered the numerator as negative to find the values of ‘x’ satisfying the given inequality.