
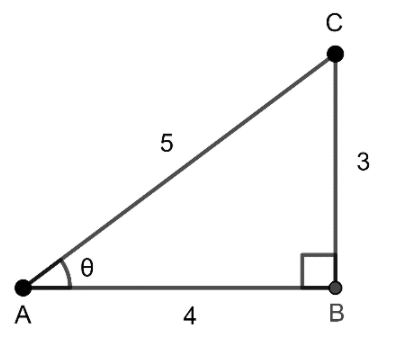
Find the six trigonometric ratios of the angle

Answer
430.5k+ views
Hint: Here in this right-angled triangle the opposite side of the angle
Complete step by step solution:
We know that there are six trigonometric ratios namely sine, cosine, tangent, cosecant, secant and cotangent. And these six trigonometric ratios are usually abbreviated as sin, cos, tan, csc, sec, cot. We are calling them as ratios as they can be expressed in terms of the sides of a right-angled triangle for a specific angle
Recall that the side opposite to the right angle in a right triangle is called the hypotenuse of the triangle. We also know that the side opposite to an angle other than right angle in a right triangle is called as the opposite side of the angle. And also, the side other than these two sides is known as the adjacent side of the angle.
From the definitions of the trigonometric ratios, we know that
In the right triangle given, we are asked to find the trigonometric ratios of the angle
Now from definitions we get
Also,
We can see that
Similarly, we get
Hence the six trigonometric ratios of the angle
Note:
Many of them get confused with the opposite and adjacent sides of a given angle from a right-angled triangle. Always remember that the side opposite to the angle, that is the side which does not contain the angle is the opposite angle. And so, the remaining another leg is the adjacent side.
Complete step by step solution:
We know that there are six trigonometric ratios namely sine, cosine, tangent, cosecant, secant and cotangent. And these six trigonometric ratios are usually abbreviated as sin, cos, tan, csc, sec, cot. We are calling them as ratios as they can be expressed in terms of the sides of a right-angled triangle for a specific angle
Recall that the side opposite to the right angle in a right triangle is called the hypotenuse of the triangle. We also know that the side opposite to an angle other than right angle in a right triangle is called as the opposite side of the angle. And also, the side other than these two sides is known as the adjacent side of the angle.
From the definitions of the trigonometric ratios, we know that
In the right triangle given, we are asked to find the trigonometric ratios of the angle
Now from definitions we get
Also,
We can see that
Similarly, we get
Hence the six trigonometric ratios of the angle
Note:
Many of them get confused with the opposite and adjacent sides of a given angle from a right-angled triangle. Always remember that the side opposite to the angle, that is the side which does not contain the angle is the opposite angle. And so, the remaining another leg is the adjacent side.
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE




