Question

Find the size of each exterior angle of a regular octagon.

Answer 1

Hint: We have been asked to find the exterior angle of a regular octagon. We know that the sum of interior angles of any polygon is \[180(n-2)\]. For a regular octagon, \[n=8\]. So, when we divide the sum of internal angles by the number of sides of a regular octagon, we will get the value of the interior angle of a regular octagon. If we subtract the interior angle by \[180\], we will get the value of each exterior angle.

Complete step by step solution:
According to the given question, we are given a regular octagon and we have to find the exterior angle.
So, we will begin by finding the sum of interior angles of a regular octagon.
We know that, for any polygon, the sum of interior angles is found using the formula \[180(n-2)\].
We will be using this formula and find the value of the sum of interior angles of a regular octagon.
We know that a regular octagon has 8 sides. And so, \[n=8\] for a regular octagon.
So, the sum of interior angles
\[\Rightarrow 180(8-2)\]
\[\Rightarrow 180(6)\]
Solving this, we get,
\[\Rightarrow 1080\]
So, the sum of the interior angle of a regular octagon is \[{{1080}^{\circ }}\].
If we divide the sum of interior angles of a polygon by the number of sides of a polygon, we will get the interior angle value of that polygon.
So for a regular octagon, the interior angle \[=\dfrac{{{1080}^{\circ }}}{8}\]\[={{135}^{\circ }}\]

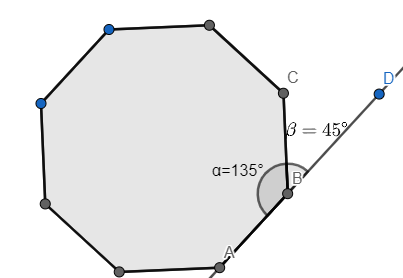
But, we have to find the value of the exterior angle of a regular octagon, so we will subtract the interior angle by \[{{180}^{\circ }}\](which is the angle subtended by a straight line).
So, we have the value of the exterior angle \[={{180}^{\circ }}-{{135}^{\circ }}={{45}^{\circ }}\]
Therefore, the value of the exterior angle is \[{{45}^{\circ }}\].

Note: For finding the sum of interior angles, make sure that the number of sides of the polygon under consideration is taken correctly.
For example – For pentagon, \[n=5\] and for hexagon, \[n=6\], etc.
When we divide the sum of the interior angles by the number of sides, we will get the value of the interior angle and so don’t confuse it with the exterior angle value.