Question

How do you find the slope and intercept to graph $x + y = - 5$?

Answer 1

Hint: Slope is the change in the value of $y$ with respect to $x$ in the equation. We can find the slope of the line by using the slope-intercept formula wherein we write the given equation in the form $y = mx + c$, where $m$ is the slope of the line and $c$ is the y-intercept.
The intercepts are the points at which the line of an equation cuts the x-axis and y-axis. At the $x$ intercept on x-axis, $y = 0$. Similarly at the y-intercept on y-axis, $x = 0$.

Complete step by step solution:
We have to find the slope of the line given by the equation $x + y = - 5$.
We will use the slope-intercept formula to find the slope of the line.
The slope-intercept formula is given by $y = mx + c$.
On rearranging the equation, we get:
$
  x + y = - 5 \\
   \Rightarrow y = - x - 5 \\
$
On comparing the equation $y = - x - 5$ with the standard form of the slope-intercept formula, we see that
$m = - 1$ and $c = - 5$
Thus, the slope of the given line is $ - 1$
Also, $c = - 5$. So, the point at which line will cut y-axis is $(0,{\kern 1pt} {\kern 1pt} - 5)$
Now, we find the x-intercept by assuming $y = 0$ in the equation and evaluate the corresponding value of $x$. We assume here $y = 0$ because that the line will touch x-axis at that point.
$
  x + y = - 5 \\
   \Rightarrow x + 0 = - 5 \\
   \Rightarrow x = - 5 \\
$
Thus, we get the point as $\left( { - 5,0} \right)$. This is the x-intercept of the graph of the given equation.
Hence, the slope of the given line is $3$, the x-intercept is $\left( { - 5,0} \right)$ and y-intercept is $(0,{\kern 1pt} {\kern 1pt} - 5)$
This can be shown by way of the graph of $x + y = - 5$.

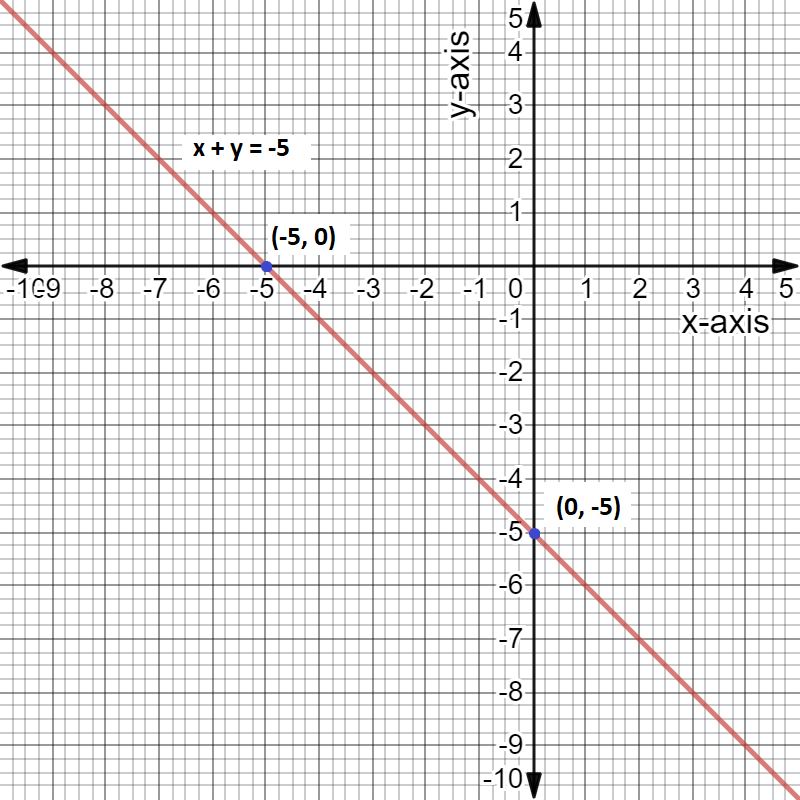
Note: For a straight line, if two points $A({x_1},{\kern 1pt} {\kern 1pt} {\kern 1pt} {y_1})$ and $B({x_2},{\kern 1pt} {\kern 1pt} {\kern 1pt} {y_2})$ are situated on the line, then by slope formula we can calculate the slope (m) as, $m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$.
For a linear equation, we can also find the intercepts by writing the equation in the form of $\dfrac{x}{a} + \dfrac{y}{b} = 1$, where $a$ will be the $x$ intercept and $b$ will be the $y$ intercept. For a linear equation in two variables we get at most one $x$ intercept and at most one $y$ intercept.