Question

Find the square root of 225.
A. 12
B. 13
C. 15
D. None of these

Answer 1

Use the rules of division method for finding the square root of the given number. Put bars to digits from the unit place by taking one bar on two digits. So, we get the number after putting bars as $\overline{2}\overline{25}$. Now, use the rules of division method and the quotient of this method is the square root of the given number.

Complete step-by-step answer:
Division method for finding square roots can be given as;
(a) First place a bar over every pair of digits starting from unit digit, if the number of digits are odd then the left most single digit will also have a bar.
(b) Think of the largest number whose square is even to just less than the first bar digit. Take this number as divisor and also as quotient.
(c) Next subtract the product of the divisor and the quotient from the first bar digit and bring down the next pair of digits which have a bar to the right side of the remainder, that becomes a new dividend.
(d) Now new divisor is obtained by adding the first divisor and the quotient and add a digit to the right side of it that we have to choose (according to the new dividend which is chosen in such a way that product of new divisor and this digit is less than or equal to the new dividend).
(e) Repeat step (b, c, d) till the bar digit has been taken up. Now quotient is taken up. Now quotient is the required square root of the given number.
Now, let us apply the above steps to find the square root of 225.
(i) First place bar at two digits starting from unit place and after that put bar at one digit remaining as well.
Hence, we get $\overline{2}\overline{25}$
(ii) Now, we observe that
$\begin{align}
  & {{1}^{2}}<2<{{2}^{2}} \\
 & \Rightarrow 1<2<4 \\
\end{align}$
So, we can take divisor and quotient as (1). So, we get,

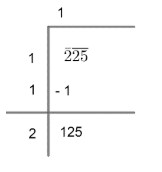
(iii) Now, we need to put the same digits to the divisor (with 2) and quotient as well. So, we can observe that
$\begin{align}
  & 21\times 1=21 \\
 & 22\times 2=44 \\
 & 23\times 3=69 \\
 & 24\times 4=96 \\
 & 25\times 5=125 \\
\end{align}$
So, we can put 5 to divisor and quotient both. So, we get,

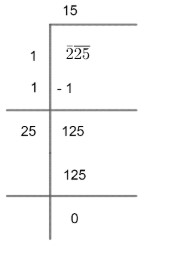
(iv) Hence, quotient ‘15’ is the square root of 225.
So, option (C) is correct.

Note: One may go wrong while putting bars from the beginning of the number 225. So, take care of it.
Another approach for calculating the square roots of 225 can be the factorization method in the following way,

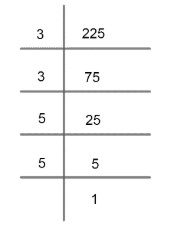
So, we get $225=3\times 3\times5\times 5 $
Square root of $225=3\times 5=15$.
Hence, it can be another way for finding square roots as well.