
Find the square root of 3481 by division method.
Answer
575.1k+ views
Hint: For finding the square root of the given number, first make pairs from the unit place. Now take the largest number whose square is equal to or just less than the number in the first bar from left. Now subtract the digit of the given number and the square of the number written in the quotient. Bring down the next pair. Then, take twice of the number taken in the first place and add the unit digit to that number such that when that unit digit is multiplied with the number formed, it is equal to less than the current dividend. Repeat the process till you get remainder as 0.
Complete step by step solution: We shall begin by making groups of 2 digits starting from the unit place.
Make the pair such as $\overline {34} \overline {81} $, there are two pairs, the first pair has 34 and second pair is 81.
Now, take the divisor as the largest number whose square is equal to or just less than the first digit in the bar from the starting digits of the given number.
As ${5^2} = 25 < 34$ and ${6^2} = 36 > 34$
Therefore, our divisor is 5. Subtract the first pair from the square of 5 and then bring the next pair down.
Now, we get,
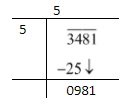
Next, our dividend is 981.
Write the twice of the first divisor, which is $5 \times 2 = 10$
We will now find the unit digit placed with 10 such that when that digit is multiplied by the new number, the result is less than or equal to the dividend.
Therefore, we have
\[109 \times 9 = 981\]
Hence, the next digit in divisor is 9.
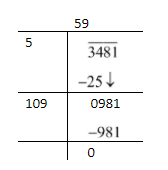
Now, the remainder is 0.
Hence, the square root of 3481 is 59.
Note: Many students make mistakes by making a pair from the starting of the number instead of a unit place, which gives the incorrect answer. Also, make sure when you bring down the digit, you take the whole pair and not the single digit.
Complete step by step solution: We shall begin by making groups of 2 digits starting from the unit place.
Make the pair such as $\overline {34} \overline {81} $, there are two pairs, the first pair has 34 and second pair is 81.
Now, take the divisor as the largest number whose square is equal to or just less than the first digit in the bar from the starting digits of the given number.
As ${5^2} = 25 < 34$ and ${6^2} = 36 > 34$
Therefore, our divisor is 5. Subtract the first pair from the square of 5 and then bring the next pair down.
Now, we get,
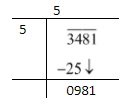
Next, our dividend is 981.
Write the twice of the first divisor, which is $5 \times 2 = 10$
We will now find the unit digit placed with 10 such that when that digit is multiplied by the new number, the result is less than or equal to the dividend.
Therefore, we have
\[109 \times 9 = 981\]
Hence, the next digit in divisor is 9.
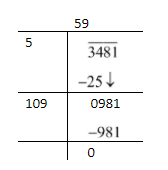
Now, the remainder is 0.
Hence, the square root of 3481 is 59.
Note: Many students make mistakes by making a pair from the starting of the number instead of a unit place, which gives the incorrect answer. Also, make sure when you bring down the digit, you take the whole pair and not the single digit.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Which one of the following groups comprises states class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

A couple went for a picnic They have 5 sons and each class 8 maths CBSE

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE




