Question

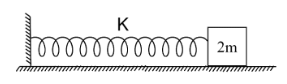
Find the time period of the following spring-mass system

(A) $ T=2\pi \sqrt{\dfrac{2m}{k}} $
(B) $ T=2\pi \sqrt{\dfrac{m}{k}} $
(C) $ T=2\pi \sqrt{\dfrac{m}{2k}} $

Answer 1

Hint :The relation between the time period of the system, the mass of the block, and spring constant of spring can be obtained by considering the restoring force for spring, the second law of motion, and acceleration for Simple Harmonic Function.

Complete Step By Step Answer:
Let us consider a system in which a block of mass $ m $ is tied to a wall through a string with a spring constant $ k $ .
Now, if the block is pulled so that the spring is stretched by a distance $ x $ , a restoring force is generated in the spring proportional to the distance $ x $ .
The restoring force of spring can be given as,
 $ F=-kx $
Now, if the block is released, it will accelerate toward the spring due to the restoring force with an acceleration $ a $ .
Hence, the force required for the object of mass $ m $ to move with acceleration $ a $ is provided by the restoring spring force.
By Newton’s second law of motion,
 $ F=ma $
This force is equal to the spring force
 $ \therefore -kx=ma $ …… $ (1) $
Now, we know that when a stretched spring is released, it contracts and expands periodically, which explains it follows the Simple Harmonic Motion.
Now, the acceleration for simple harmonic motion is given as
 $ a=-{{\omega }^{2}}x $ , where $ \omega $ is the angular frequency of the motion.
Substituting the value of acceleration in the equation $ (1) $ ,
 $ \therefore -kx=m(-{{\omega }^{2}}x) $
Canceling the negative sign and the common terms on both sides,
 $ \therefore k=m{{\omega }^{2}} $
 $ \therefore \dfrac{k}{m}={{\omega }^{2}} $
Applying square root on both sides,
 $ \therefore \omega =\sqrt{\dfrac{k}{m}} $
Now, we know that the angular frequency can be represented in terms of the time period as
 $ \omega =\dfrac{2\pi }{T} $
Substituting the value,
 $ \therefore \dfrac{2\pi }{T}=\sqrt{\dfrac{k}{m}} $
 $ \therefore T=2\pi \sqrt{\dfrac{m}{k}} $
This is the relation between the time period, the mass of the block, and the spring constant.
For the given question,
Mass of block = $ 2\;m $
Spring constant = $ k $
Substituting these values in the obtained equation,
 $ \therefore T=2\pi \sqrt{\dfrac{2m}{k}} $
Thus, the correct answer is Option $ (A) $ .

Note :
The obtained equation for the time period of a spring-block system is a general equation that can be used even when more than one spring is attached in series or parallel manner.
The acceleration of the oscillations can be derived from the general equation of SHM $ y=A\sin (\omega t+\phi ) $ .