Find the transverse common tangent of the circles.${{x}^{2}}+{{y}^{2}}-4x-10y+28=0\,\,and\,{{x}^{2}}+{{y}^{2}}+4x-6y+4=0$.
Answer
Verified457.5k+ views
Hint: Find the centre and radius of both the given circles by comparing their equation with the standard equation of circle. Then find the distance between their centres and sum of their radii. Check whether ${{c}_{1}}{{c}_{2}}$ (distance) > ${{r}_{1}}{{r}_{2}}$ or not and then draw their transverse tangents accordingly. Using a rough figure. After that find the point of intersection of tangents a slope of the tangents with the help of given conditions. After that write an equation of tangents using point-slope form.
Therefore in this case there will be four common tangents line QR and ST are called transverse common tangents and these lines ${{c}_{1}}{{c}_{2}}$ on P and P divides the line ${{c}_{1}}{{c}_{2}}$ in the ratio of \[{{r}_{1}}:{{r}_{2}}\] internally.
Complete step by step answer:
Given circles are - ${{c}_{1\,}}and\,{{c}_{2}}$ I.e. ${{x}^{2}}+{{y}^{2}}-4x-10y+28=0\,\,and\,{{x}^{2}}+{{y}^{2}}+4x-6y+4=0$. Compare these equations with the standard equation of the circle to find the centres and radius of the circles.
Standard equation of the circle is- $x^2+y^2+2gx+2fy+c=0$
Comparing circle 1 with the standard solution we get centre of the circle 1 as $(-g,-f)$
${{x}^{2}}+{{y}^{2}}-4x-10y+28=0$
2g= - 4,
g= - 2,
2f= - 10,
f= (-5)
c= 28
Here, centre = (2,5)
Its radius = $\sqrt{{{f}^{2}}+{{g}^{2}}-c}\,=\,\sqrt{4+25-28}\,=1\,units$
Now, we will compare the equation of circle 2 with the standard equation of circle.
Now for ${{x}^{2}}+{{y}^{2}}+4x-6y+4=0$
2g= 4,
g= 2,
2f= - 6,
f= (-3)
c = 4
Hence, centre=$ (-g,-f) = (-2,3)$
Radius of circle is
$\begin{align}
& \sqrt{{{g}^{2}}+{{f}^{2}}-{{c}^{2}}} \\
& =\sqrt{4+9-4} \\
& =3\,units \\
\end{align}$
Now, we will find the distance between centres of the two-circles using distance formula.
Distance between two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$
\[=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]
Therefore, distance between ${{c}_{1}}\left( 2,5 \right)\,\,and\,{{c}_{2}}(-2,3)$
\[\begin{align}
& {{c}_{1}}{{c}_{2}}=\sqrt{{{\left[ +2-\left( -2 \right) \right]}^{2}}+{{\left( 5-3 \right)}^{2}}.........} \\
& {{c}_{1}}{{c}_{2}}=\sqrt{{{\left( 4 \right)}^{2}}+{{\left( 2 \right)}^{2}}} \\
& {{c}_{1}}{{c}_{2}}=\sqrt{16+4} \\
& {{c}_{1}}{{c}_{2}}=\sqrt{20} \\
\end{align}\]
We have $\left( {{r}_{1}}+{{r}_{2}} \right)=\left( 1+3 \right)=4\,Units$
Therefore, we have \[{{c}_{1}}{{c}_{2}}>{{r}_{1}}+{{r}_{2}}\] , \[\because \left[ \sqrt{20}>4 \right]\] .
Now, we know that if the distance between the centres of two circles is greater than the sum of their radii, then two transverse common tangents are possible. Hence, we can draw the following diagram:
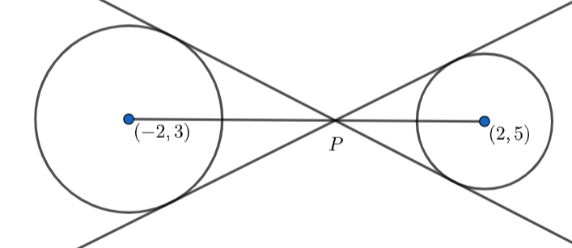
We know, the transverse tangents and the line joining the centres of the circle are concurrent and the point of concurrency divides the line joining the centres ${{c}_{1}}$ and ${{c}_{2}}$ in the ratio ${{r}_{1}}:{{r}_{2}}$ . So, the point P divides the line joining the centres (2,5) and (-2,3) in the ratio 1:3.
Now, we know the coordinates of the point dividing the line joining the points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ in the ratio m:n is given as $(x,y)=\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)$ .
So, P = $\left( \dfrac{\left( 2\times 3 \right)+\left( -2\times 1 \right)}{3+1},\dfrac{\left( 5\times 3 \right)+\left( 3\times 1 \right)}{3+1} \right)$
$\Rightarrow P=\left( \dfrac{6-2}{4},\dfrac{15+3}{4} \right)$
$\Rightarrow P=\left( \dfrac{4}{4},\dfrac{18}{4} \right)$
$\Rightarrow P=\left( 1,\dfrac{9}{2} \right)$
Now, we can find equation of tangent having slope “m” and passing through point $\left(1, \dfrac 92\right)$
$=y-{{y}_{0}}=m\left( x-{{x}_{0}} \right)$ {equation of straight-line having slope m and passing through point $\left( {{x}_{0}},{{y}_{0}} \right)$}
\[\begin{align}
& y-\dfrac{9}{2}=m\left( x-1 \right) \\
& \Rightarrow \dfrac{2y-9}{2}=m\left( x-1 \right) \\
& \Rightarrow 2y-9=2m\left( x-1 \right) \\
& \Rightarrow 2y-9=2mx-2m \\
& \Rightarrow 2mx-2y+9-2m=0........(i) \\
\end{align}\]
The above equation(i) represents the equation of tangent to circle ${{x}^{2}}+{{y}^{2}}-4x-10y+28=0$.
We know, the line joining the centre to the point of contact of tangent is perpendicular to the tangent. So, the perpendicular distance of the centre from the tangent is equal to the radius of the circle. This is calculated by using the formula given as the distance from a point (m,n) to the line $ax+by+c=0$ is given by:
\[d=\dfrac{\left| am+bn+c \right|}{\sqrt{{{a}^{2}}-{{b}^{2}}}}\]
Now, for the circle \[{{x}^{2}}+{{y}^{2}}-4x-10y+28=0\],
Radius of this circle= distance from centre (2,5) to the tangent
$\Rightarrow 1=\dfrac{2m\left( 2 \right)-2\left( 5 \right)+9-2m}{\sqrt{{{\left( 2m \right)}^{2}}+{{\left( 2 \right)}^{2}}}}$
$\Rightarrow 1=\dfrac{2m\left( 2 \right)-10+9-2m}{\sqrt{4{{m}^{2}}+4}}$
$\Rightarrow 1=\dfrac{2m-1}{\sqrt{4{{m}^{2}}+4}}$
\[\Rightarrow 2\sqrt{{{m}^{2}}+1}=4m-2m-1\]
\[\Rightarrow 4\left( {{m}^{2}}+1 \right)={{\left( 2m-1 \right)}^{2}}\]
\[\Rightarrow 4{{m}^{2}}+4=4{{m}^{2}}+1-4m\]
\[\Rightarrow 4=1-4m\]
\[\Rightarrow 4m=1-4\]
\[\Rightarrow 4m=\left( -3 \right)\]
\[\therefore m=\dfrac{-3}{4}\]
Since, we have two tangents passing from point $\left(1, \dfrac 92\right)$ , there should be two values of m. But ${{m}^{2}}$ term is eliminated. So, the coefficient of ${{m}^{2}}$= 0. So, the product of roots of the equation will be equal to $\infty $, which is possible only if the other slope is $\infty $.
$\therefore $Slope of other tangent line is $\infty $,
Now, equation of tangent having slope $\dfrac{-3}{4}$ and which passes through point $\left(1, \dfrac 92\right)$ is
$\begin{align}
& y-9=\dfrac{-3}{4}\left( x-1 \right) \\
& \Rightarrow \dfrac{2y-9}{2}=\dfrac{-3}{4}\left( x-1 \right) \\
& \Rightarrow 4\left( 2y-9 \right)=-6\left( x-1 \right) \\
& \Rightarrow 8y-36=-6x+6 \\
& \Rightarrow 8y+6x-36-6=0 \\
& \Rightarrow 6x+8y-42=0 \\
& \Rightarrow 3x+4y-21=0\, \\
\end{align}$
Now, the equation of the tangent line having slope $\infty $ and passing through $\left(1, \dfrac 92\right)$ is $x=1. $
Hence, equation of transverse common tangents of the circle ${{x}^{2}}+{{y}^{2}}-4x-10y+28=0$ and ${{x}^{2}}+{{y}^{2}}+4x-6y+4=0$ are:
$3x+4y-21=0\,\,and\,\,x=1$ .
Note: The number of transverse common tangents between two circles can be found out using the following conditions:
(i) If the distance between the centres is more than the sum of the radii of the circles, then the number of transverse common tangents is 2.
(ii) If the distance between the centres is equal to the sum of the radii of the circles, then the number of transverse common tangents is 1.
(iii) If the distance between the centres is less than the sum of the radii of the circles, then the number of transverse common tangents is 0.
Therefore in this case there will be four common tangents line QR and ST are called transverse common tangents and these lines ${{c}_{1}}{{c}_{2}}$ on P and P divides the line ${{c}_{1}}{{c}_{2}}$ in the ratio of \[{{r}_{1}}:{{r}_{2}}\] internally.
Complete step by step answer:
Given circles are - ${{c}_{1\,}}and\,{{c}_{2}}$ I.e. ${{x}^{2}}+{{y}^{2}}-4x-10y+28=0\,\,and\,{{x}^{2}}+{{y}^{2}}+4x-6y+4=0$. Compare these equations with the standard equation of the circle to find the centres and radius of the circles.
Standard equation of the circle is- $x^2+y^2+2gx+2fy+c=0$
Comparing circle 1 with the standard solution we get centre of the circle 1 as $(-g,-f)$
${{x}^{2}}+{{y}^{2}}-4x-10y+28=0$
2g= - 4,
g= - 2,
2f= - 10,
f= (-5)
c= 28
Here, centre = (2,5)
Its radius = $\sqrt{{{f}^{2}}+{{g}^{2}}-c}\,=\,\sqrt{4+25-28}\,=1\,units$
Now, we will compare the equation of circle 2 with the standard equation of circle.
Now for ${{x}^{2}}+{{y}^{2}}+4x-6y+4=0$
2g= 4,
g= 2,
2f= - 6,
f= (-3)
c = 4
Hence, centre=$ (-g,-f) = (-2,3)$
Radius of circle is
$\begin{align}
& \sqrt{{{g}^{2}}+{{f}^{2}}-{{c}^{2}}} \\
& =\sqrt{4+9-4} \\
& =3\,units \\
\end{align}$
Now, we will find the distance between centres of the two-circles using distance formula.
Distance between two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$
\[=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]
Therefore, distance between ${{c}_{1}}\left( 2,5 \right)\,\,and\,{{c}_{2}}(-2,3)$
\[\begin{align}
& {{c}_{1}}{{c}_{2}}=\sqrt{{{\left[ +2-\left( -2 \right) \right]}^{2}}+{{\left( 5-3 \right)}^{2}}.........} \\
& {{c}_{1}}{{c}_{2}}=\sqrt{{{\left( 4 \right)}^{2}}+{{\left( 2 \right)}^{2}}} \\
& {{c}_{1}}{{c}_{2}}=\sqrt{16+4} \\
& {{c}_{1}}{{c}_{2}}=\sqrt{20} \\
\end{align}\]
We have $\left( {{r}_{1}}+{{r}_{2}} \right)=\left( 1+3 \right)=4\,Units$
Therefore, we have \[{{c}_{1}}{{c}_{2}}>{{r}_{1}}+{{r}_{2}}\] , \[\because \left[ \sqrt{20}>4 \right]\] .
Now, we know that if the distance between the centres of two circles is greater than the sum of their radii, then two transverse common tangents are possible. Hence, we can draw the following diagram:
We know, the transverse tangents and the line joining the centres of the circle are concurrent and the point of concurrency divides the line joining the centres ${{c}_{1}}$ and ${{c}_{2}}$ in the ratio ${{r}_{1}}:{{r}_{2}}$ . So, the point P divides the line joining the centres (2,5) and (-2,3) in the ratio 1:3.
Now, we know the coordinates of the point dividing the line joining the points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ in the ratio m:n is given as $(x,y)=\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)$ .
So, P = $\left( \dfrac{\left( 2\times 3 \right)+\left( -2\times 1 \right)}{3+1},\dfrac{\left( 5\times 3 \right)+\left( 3\times 1 \right)}{3+1} \right)$
$\Rightarrow P=\left( \dfrac{6-2}{4},\dfrac{15+3}{4} \right)$
$\Rightarrow P=\left( \dfrac{4}{4},\dfrac{18}{4} \right)$
$\Rightarrow P=\left( 1,\dfrac{9}{2} \right)$
Now, we can find equation of tangent having slope “m” and passing through point $\left(1, \dfrac 92\right)$
$=y-{{y}_{0}}=m\left( x-{{x}_{0}} \right)$ {equation of straight-line having slope m and passing through point $\left( {{x}_{0}},{{y}_{0}} \right)$}
\[\begin{align}
& y-\dfrac{9}{2}=m\left( x-1 \right) \\
& \Rightarrow \dfrac{2y-9}{2}=m\left( x-1 \right) \\
& \Rightarrow 2y-9=2m\left( x-1 \right) \\
& \Rightarrow 2y-9=2mx-2m \\
& \Rightarrow 2mx-2y+9-2m=0........(i) \\
\end{align}\]
The above equation(i) represents the equation of tangent to circle ${{x}^{2}}+{{y}^{2}}-4x-10y+28=0$.
We know, the line joining the centre to the point of contact of tangent is perpendicular to the tangent. So, the perpendicular distance of the centre from the tangent is equal to the radius of the circle. This is calculated by using the formula given as the distance from a point (m,n) to the line $ax+by+c=0$ is given by:
\[d=\dfrac{\left| am+bn+c \right|}{\sqrt{{{a}^{2}}-{{b}^{2}}}}\]
Now, for the circle \[{{x}^{2}}+{{y}^{2}}-4x-10y+28=0\],
Radius of this circle= distance from centre (2,5) to the tangent
$\Rightarrow 1=\dfrac{2m\left( 2 \right)-2\left( 5 \right)+9-2m}{\sqrt{{{\left( 2m \right)}^{2}}+{{\left( 2 \right)}^{2}}}}$
$\Rightarrow 1=\dfrac{2m\left( 2 \right)-10+9-2m}{\sqrt{4{{m}^{2}}+4}}$
$\Rightarrow 1=\dfrac{2m-1}{\sqrt{4{{m}^{2}}+4}}$
\[\Rightarrow 2\sqrt{{{m}^{2}}+1}=4m-2m-1\]
\[\Rightarrow 4\left( {{m}^{2}}+1 \right)={{\left( 2m-1 \right)}^{2}}\]
\[\Rightarrow 4{{m}^{2}}+4=4{{m}^{2}}+1-4m\]
\[\Rightarrow 4=1-4m\]
\[\Rightarrow 4m=1-4\]
\[\Rightarrow 4m=\left( -3 \right)\]
\[\therefore m=\dfrac{-3}{4}\]
Since, we have two tangents passing from point $\left(1, \dfrac 92\right)$ , there should be two values of m. But ${{m}^{2}}$ term is eliminated. So, the coefficient of ${{m}^{2}}$= 0. So, the product of roots of the equation will be equal to $\infty $, which is possible only if the other slope is $\infty $.
$\therefore $Slope of other tangent line is $\infty $,
Now, equation of tangent having slope $\dfrac{-3}{4}$ and which passes through point $\left(1, \dfrac 92\right)$ is
$\begin{align}
& y-9=\dfrac{-3}{4}\left( x-1 \right) \\
& \Rightarrow \dfrac{2y-9}{2}=\dfrac{-3}{4}\left( x-1 \right) \\
& \Rightarrow 4\left( 2y-9 \right)=-6\left( x-1 \right) \\
& \Rightarrow 8y-36=-6x+6 \\
& \Rightarrow 8y+6x-36-6=0 \\
& \Rightarrow 6x+8y-42=0 \\
& \Rightarrow 3x+4y-21=0\, \\
\end{align}$
Now, the equation of the tangent line having slope $\infty $ and passing through $\left(1, \dfrac 92\right)$ is $x=1. $
Hence, equation of transverse common tangents of the circle ${{x}^{2}}+{{y}^{2}}-4x-10y+28=0$ and ${{x}^{2}}+{{y}^{2}}+4x-6y+4=0$ are:
$3x+4y-21=0\,\,and\,\,x=1$ .
Note: The number of transverse common tangents between two circles can be found out using the following conditions:
(i) If the distance between the centres is more than the sum of the radii of the circles, then the number of transverse common tangents is 2.
(ii) If the distance between the centres is equal to the sum of the radii of the circles, then the number of transverse common tangents is 1.
(iii) If the distance between the centres is less than the sum of the radii of the circles, then the number of transverse common tangents is 0.
Recently Updated Pages
Master Class 11 English: Engaging Questions & Answers for Success
Master Class 11 Computer Science: Engaging Questions & Answers for Success
Master Class 11 Maths: Engaging Questions & Answers for Success
Master Class 11 Social Science: Engaging Questions & Answers for Success
Master Class 11 Economics: Engaging Questions & Answers for Success
Master Class 11 Business Studies: Engaging Questions & Answers for Success
Trending doubts
10 examples of friction in our daily life
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE
Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE
State and prove Bernoullis theorem class 11 physics CBSE
Pigmented layer in the eye is called as a Cornea b class 11 biology CBSE
What problem did Carter face when he reached the mummy class 11 english CBSE