
How do you find the turning points of a cubic function?
Answer
463.2k+ views
Hint: The gradient of the turning point of a curve is found by calculating the gradient of the tangent of that point. These tangents have positive and negative gradients. The horizontal tangents have zero gradient. The point which is at zero gradient is called the turning point.
Complete step by step solution:
Here, we will take an example, we will solve an equation to know how to find the turning point of a cubic function. The equation is
First, we have to differentiate the given cubic equation. This will give us the derivative. The derivative is the rate of change of function at a point equivalent to the tangent drawn.
Each term of the cubic equation is in the form of
Applying this rule to the terms in the cubic equations, which is differentiating the first term of the equation
On differentiating the second term of the equation we get,
On differentiating the third term of the equation we get,
Finally, differentiating the last term of the equation, we get,
The turning point of the gradient is
This is a quadratic equation. To solve this quadratic equation, we will use the formula for the quadratic equation which is,
Now comparing both the quadratic equations we get that
Putting the values of
When we put the value of
This gives us the first value of the turning point:
Turning point =
Then we need to substitute the second value of
So, now turning point =
Now, we will graph the points in the graph paper and see what kind of curve we get.
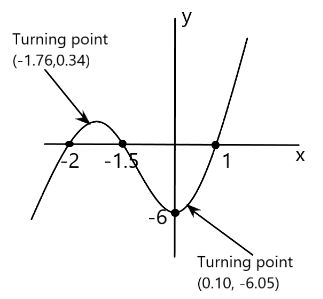
So, this is how we find the turning points of a cubic function and make the graph.
Note: The above method is easy to solve. But there is another method. It is called the Hit and Trial Method in which we take our desired values and put that in the equation and try to solve. Generally the values which we take should be the values which are more prone to be correct.
Complete step by step solution:
Here, we will take an example, we will solve an equation to know how to find the turning point of a cubic function. The equation is
First, we have to differentiate the given cubic equation. This will give us the derivative. The derivative is the rate of change of function at a point equivalent to the tangent drawn.
Each term of the cubic equation is in the form of
Applying this rule to the terms in the cubic equations, which is differentiating the first term of the equation
On differentiating the second term of the equation we get,
On differentiating the third term of the equation we get,
Finally, differentiating the last term of the equation, we get,
The turning point of the gradient is
This is a quadratic equation. To solve this quadratic equation, we will use the formula for the quadratic equation which is,
Now comparing both the quadratic equations we get that
Putting the values of
When we put the value of
This gives us the first value of the turning point:
Turning point =
Then we need to substitute the second value of
So, now turning point =
Now, we will graph the points in the graph paper and see what kind of curve we get.

So, this is how we find the turning points of a cubic function and make the graph.
Note: The above method is easy to solve. But there is another method. It is called the Hit and Trial Method in which we take our desired values and put that in the equation and try to solve. Generally the values which we take should be the values which are more prone to be correct.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




