
Find the value of
A)
B)
C)
D)
Answer
481.8k+ views
Hint: Here, we are required to find the value of
Complete step by step solution:
Now, we will draw the quadrants:
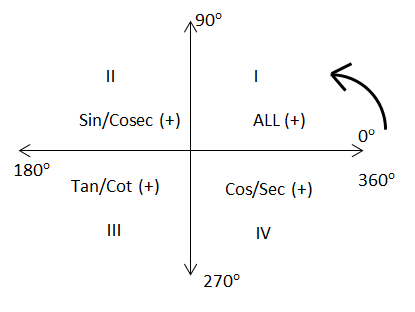
Now,
Since,
Therefore,
Now, when we add any angle to
Since,
Now, this can be written as:
Now, we can find the value of
Now, when we subtract any angle from
In the second quadrant, cosine is negative and due to
As we know,
Hence,
Now, when we subtract any angle from
In the third quadrant, cosine is negative and also, due to
As we know,
Hence,
Therefore, the value of
Hence,
Therefore, the required answer is
And, option D is the correct answer.
Note:
We should take care while solving the quadrants because in one quadrant cosine is positive and in the other it is negative. If we use
Complete step by step solution:
Now, we will draw the quadrants:

Now,
Since,
Therefore,
Now, when we add any angle to
Since,
Now, this can be written as:
Now, we can find the value of
Now, when we subtract any angle from
In the second quadrant, cosine is negative and due to
As we know,
Hence,
Now, when we subtract any angle from
In the third quadrant, cosine is negative and also, due to
As we know,
Hence,
Therefore, the value of
Hence,
Therefore, the required answer is
And, option D is the correct answer.
Note:
We should take care while solving the quadrants because in one quadrant cosine is positive and in the other it is negative. If we use
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the full form of POSCO class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

Discuss the main reasons for poverty in India




