Question

Find the value of $\lambda $ for which the lines:
$y = x + 1$, $y = \lambda x + 2$ and $y = ({\lambda ^2} + \lambda - 1)x + 3$ are concurrent

Answer 1

Hint: If the three lines are given:
${A_1}x + {B_1}y + {c_1} = 0$, ${A_2}x + {B_2}y + {c_2} = 0$ and ${A_3}x + {B_3}y + {c_3} = 0$ are concurrent then the determinant of their coefficients is zero.
$\left| {\begin{array}{*{20}{c}}
  {{A_1}}&{{B_1}}&{{c_1}} \\
  {{A_2}}&{{B_2}}&{{c_2}} \\
  {{A_3}}&{{B_3}}&{{c_3}}
\end{array}} \right| = 0$

Complete step-by-step answer:
Concurrent lines are those lines which meet or intersect at the same point.
For example: different lines ${L_1},{L_2},{L_3},{L_4},{L_5}$ are given

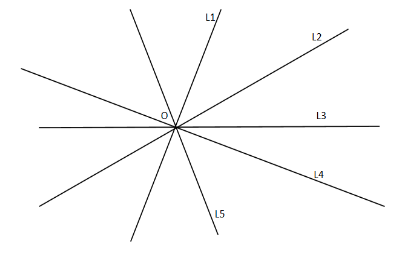
All these lines intersect at a single point $O$ so we can say that all these three lines are concurrent and hence $O$ is called the point of concurrency.
For any given three lines, the determinant of their coefficients gives the area of the quadrilateral but for the non-concurrent lines area would be zero. So firstly we need to write the given line in
${A_1}x + {B_1}y + {c_1} = 0$, ${A_2}x + {B_2}y + {c_2} = 0$ and ${A_3}x + {B_3}y + {c_3} = 0$
So in the first equation, we are given $y = x + 1$ and this can be written as $y - x - 1 = 0$
Second equation is given as $y = \lambda x + 2$ which can be written as $y - \lambda x - 2 = 0$
Third equation which is given as$y = ({\lambda ^2} + \lambda - 1)x + 3$
Which is given as $y - ({\lambda ^2} + \lambda - 1)x - 3 = 0$
So the determinant of the coefficient is $0$
So $\left| {\begin{array}{*{20}{c}}
  {{A_1}}&{{B_1}}&{{c_1}} \\
  {{A_2}}&{{B_2}}&{{c_2}} \\
  {{A_3}}&{{B_3}}&{{c_3}}
\end{array}} \right| = 0$
Which is written as
$\left| {\begin{array}{*{20}{c}}
  1&{ - 1}&{ - 1} \\
  1&{ - \lambda }&{ - 2} \\
  1&{ - ({\lambda ^2} + \lambda - 1)}&{ - 3}
\end{array}} \right| = 0$
Now on expanding the determinant, we get
$\Rightarrow$$1(( - \lambda )( - 3) - ( - 2)( - ({\lambda ^2} + \lambda - 1)) + 1(1( - 3) - (1)( - 2)) - 1(( - 1)({\lambda ^2} + \lambda - 1) - 1( - \lambda )) = 0$
Upon simplification, we get
$\Rightarrow$$1(3\lambda - 2({\lambda ^2} + \lambda - 1)) + 1( - 3 + 2) - 1( - ({\lambda ^2} + \lambda - 1) + \lambda ) = 0$
So further simplifying, we get
$\Rightarrow$$(3\lambda - 2{\lambda ^2} - 2\lambda + 2) - 1 - 1( - {\lambda ^2} - \lambda + 1 + \lambda ) = 0$
$\Rightarrow$$\lambda - 2{\lambda ^2} + 2 - 1 + {\lambda ^2} + 1 = 0$
$\Rightarrow$$ - {\lambda ^2} + \lambda = 0$
Taking $\lambda $ common
$\Rightarrow$$\lambda ( - \lambda + 1) = 0$
$\Rightarrow$So $\lambda = 0,1$.

For the values 0 and 1 the lines are concurrent.

Note: If we are given that the two lines are consistent, for example: ${A_1}x + {B_1}y + {c_1} = 0$, ${A_2}x + {B_2}y + {c_2} = 0$ are consistent, then it means that
$\dfrac{{{A_1}}}{{{A_2}}} \ne \dfrac{{{B_1}}}{{{B_2}}}$
If $\dfrac{{{A_1}}}{{{A_2}}} = \dfrac{{{B_1}}}{{{B_2}}}$ is given then it means that the lines are inconsistent.