Question

Find the value of the expression $\cos {{570}^{\circ }}$.

Answer 1

Hint: Cosine function is positive in 1st and 4th quadrant and negative in 2nd and 3rd quadrant. And if the angle inside the trigonometric function is of type $\dfrac{n\pi }{2}\pm \theta $ (where n is an odd), then change cos to sin, otherwise if angle is of type $n\pi \pm \theta $ , then do not change the trigonometric function, use these rules to solve the given problem. Use the value of $\cos \dfrac{\pi }{6}$ as $\dfrac{\sqrt{3}}{2}$ .

Complete step-by-step answer:

Given expression in the problem is $\cos {{570}^{\circ }}$

Let us suppose the value of the given expression is ‘M’ we can write equation as

M = $\cos {{570}^{\circ }}............\left( i \right)$

Now we can observe that the angle involved in the above expression is not lying in ${{0}^{\circ }}$ to ${{90}^{\circ }}$ i.e. not acute angle and we have known values of trigonometric function only in ${{0}^{\circ }}$ to ${{90}^{\circ }}$ . It means we have to convert the given angle to acute angle form with the help of some trigonometric identities.
Hence, let us divide the given expression by ${{180}^{\circ }}$ , so, that we can write the given angle in form of sum of angle which is multiple of ${{180}^{\circ }}$ in following way:

${{570}^{\circ }}={{180}^{\circ }}\times 3+{{30}^{\circ }}...............\left( ii \right)$

Now, as we know the radian representation of ${{180}^{\circ }}$ is given as

$\pi $ radian = ${{180}^{\circ }}...............\left( iii \right)$

And with the help of above relation, we can rewrite the angle ${{30}^{\circ }}$ in radian form as well, given as

${{30}^{\circ }}=\dfrac{\pi }{6}radian..............\left( iv \right)$

Hence, we can rewrite the expression (ii) with the help of equations (iii) and (iv) as

$570=3\pi +\dfrac{\pi }{6}................\left( v \right)$

Now, we can put the angle ${{570}^{\circ }}$ as $3\pi +\dfrac{\pi }{6}$ to the equation(i). So, we get

$M=\cos \left( 3\pi +\dfrac{\pi }{6} \right)............\left( v \right)$

Now, as we know the quadrant angles are defined as

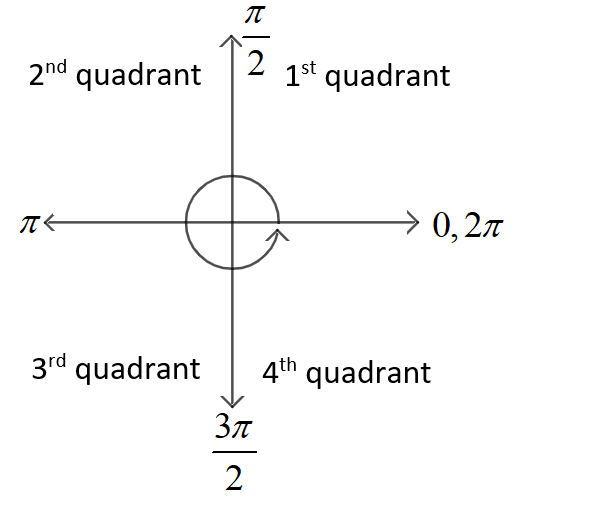
Now, we can apply the trigonometric rules for conversion of trigonometric expressions by changing its angle.

Now, we can observe that the angle $\left( 3\pi +\dfrac{\pi }{6} \right)$ will lie in 3rd quadrant because angle $3\pi $ will lie at the same position where $\pi $is lying if we rotate ${{360}^{\circ }}$ or $2\pi $ from the position of $\pi $ , and we are adding $\dfrac{\pi }{6}$ to $3\pi $ ,it means the result will lie in 3rd quadrant.

Now, as the angle is lying in the third quadrant and we know very well, cosine function is negative in the third quadrant, so conversion of cos by changing angle will affect the sign of resultant and hence, we get negative sign while conversion.

And as the angle $\left( 3\pi +\dfrac{\pi }{6} \right)$ is written by involvement of angle $3\pi $ which is a multiple of $'\pi '$ , it means the trigonometric function will remain same as per the rules of conversion of trigonometric functions by changing their angles.

Hence, we can write the identities according to the above concepts as

$\begin{align}

  & \cos \left( \pi +\theta \right)=-\cos \theta \\

 & \cos \left( 3\pi +\theta \right)=-\cos \theta \\

 & \cos \left( 5\pi +\theta \right)=-\cos \theta \\

 & \text{. }\text{. }\text{. }\text{. }\text{.} \\

 & \text{. }\text{. }\text{. }\text{. }\text{.} \\

 & \text{. }\text{. }\text{. }\text{. }\text{.} \\

 & \text{. }\text{. }\text{. }\text{. }\text{.} \\

 & \cos \left( n\pi +\theta \right)=-\cos \theta \\

\end{align}$

Where, n is an odd integer.

Hence, using the equation(vi), we get

$M=\cos \left( 3\pi +\dfrac{\pi }{6} \right)=-\cos \dfrac{\pi }{6}$

Now, we know the value of $\cos \dfrac{\pi }{6}$ is $\dfrac{\sqrt{3}}{2}$ ; so, we get

$M=-\dfrac{\sqrt{3}}{2}$

$\cos {{570}^{\circ }}=\dfrac{-\sqrt{3}}{2}$

Hence, $\dfrac{-\sqrt{3}}{2}$ is the answer.

Note: One can apply the trigonometric identity with the given expression directly without changing the angles in radian form. It is done in the solution because we are more familiar with the trigonometric relation given in solution in radian form only. So, don’t confuse with that part of the solution, you can evaluate the given expression by using degree of angle as well.
We can write $\cos 570$ as $\cos \left( 7\times 70-60 \right)$ and hence, we can get value of this expression as $\cos \left( 7\pi -60 \right)=-\sin {{60}^{\circ }}=\dfrac{-\sqrt{3}}{2}$