Question

Find the value of the unknown interior angle x in the following figure.

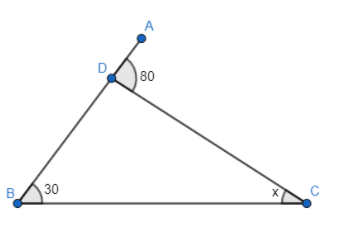
Answer 1

Hint: Use the property that the exterior angle of a triangle is equal to the sum of the opposite interior angles of a triangle. So, for the above figure, $\angle ADC$ is one of the exterior angles of the triangle given and $\angle ABC,\angle ACB$ are its opposite interior angle. So, form the mathematical equation and solve to get the value of x.

Complete step-by-step answer:
Let us start the solution to the above question by drawing the diagram given in the question.

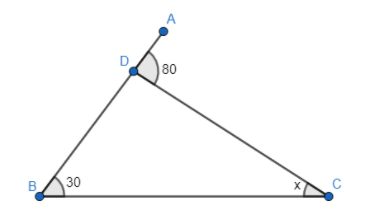
We know that the exterior angle of a triangle is equal to the sum of the opposite interior angles of a triangle. In the above figure, $\angle ADC$ is one of the exterior angles of the triangle given and $\angle ABC,\angle ACB$ are its opposite interior angle, so we can say that $\angle ADC$ is the sum of $\angle ABC\text{ and }\angle ACB$ . Also, it is given in the question that $\angle ADC=80{}^\circ $ , $\angle ABC=30{}^\circ \text{ and }\angle ACB=x$ . So, if we represent this mathematically, we get
$\angle ADC=\angle ABC\text{ + }\angle ACB$
$\Rightarrow 80=30+x$
If we take 30 to the other side of the equation, the sign changes. So, we get
$80-30=x$
$x=50$
Therefore, we can conclude that the measure of x is equal to $50{}^\circ $ .

Note:Generally, it is seen that whenever a student is asked about the exterior angle of the triangle, they misinterpret it as the corresponding interior angle subtracted from $360{}^\circ $ , while the correct concept is the corresponding interior angle subtracted from $180{}^\circ $ . If you want you can solve the above question by using the angle sum property of a triangle followed by the property of a linear pair of angles, but that would be lengthier than the above process.