Question

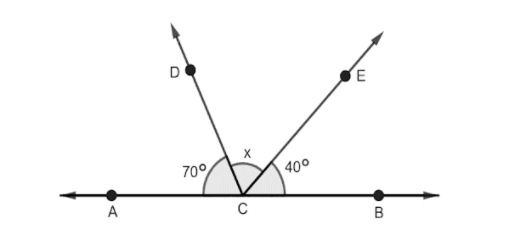
Find the value of x:

Answer 1

Hint: Here in this question, we have to find the value of angle x in the given figure. We saw a straight angle between the ray A and B whose angle is \[{180^0}\] at point C, and two more rays D and E which also passes from point C. on subtracting the angle made by D and E from a straight angle we get the required angle x.

Complete step by step solution:
A straight angle is an angle, whose vertex point has a value of \[{180^0}\] degrees. Basically, it forms a straight line, whose sides lie in opposite directions from the vertex. It is also termed as “flat angles”.
Consider, the given figure
Ray A and B passes from Point C in opposite direction and make an straight line, the angle between two rays are \[{180^0}\], and
The two rays D and E which pass from the same point C. Given the angle between rays D and A is \[{70^0}\] and the angle between rays E and B is \[{40^0}\].
We have to find the angle between the ray D and E i.e., x, by subtracting the given two angles from a straight angle \[{180^0}\].
\[ \Rightarrow x = {180^0} - {70^0} - {40^0}\]
\[ \Rightarrow x = {180^0} - {110^0}\]
On subtracting, we get
\[ \Rightarrow x = {70^0}\]
Therefore, the angle between the rays A and E is \[x = {70^0}\].
So, the correct answer is “\[x = {70^\circ}\]”.

Note: Remember, when the arms or rays of the angle lie in the opposite direction, they form a straight angle means a horizontal line and a vertical line are always straight lines and therefore they are examples of straight angles it makes an angle \[{180^0}\] is also known as linear angle.