Question

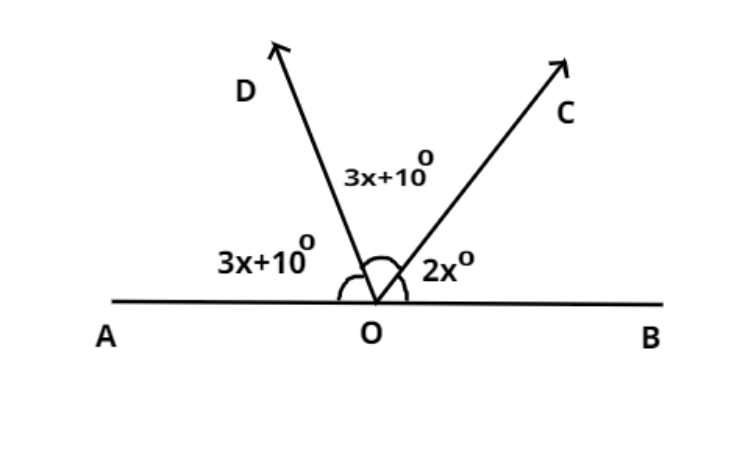
Find the value of x, so that AOB is a straight line.

Answer 1

Hint – In this question use the concept that If OAB is a line then the $\angle AOB$ must be 1800. $\angle AOB$ is the sum of angle $\angle AOD$, angle $\angle DOC$ and angle $\angle COB$, equate this addition to 180, this will give the value of x.

Complete Step-by-Step solution:
If OAB is a line then the angle AOB must be 180.
$ \Rightarrow \angle AOB = {180^0}$
Now from figure this angle is written as
$ \Rightarrow \angle AOB = {180^0} = \angle AOD + \angle DOC + \angle COB$............................ (1)
Now from figure
$\angle AOD = 3x + {10^0}$, $\angle DOC = 3x + {10^0}$, $\angle COB = 2{x^0}$
Now from equation (1) we have,
$ \Rightarrow {180^0} = 3x + {10^0} + 3x + {10^0} + 2{x^0}$
$ \Rightarrow 8x + {20^0} = {180^0}$
$ \Rightarrow 8x = {180^0} - {20^0} = {160^0}$
$ \Rightarrow x = \dfrac{{{{160}^0}}}{8} = {20^0}$
So the value of x is $20^0$ so that AOB is a line.
So this is the required answer.

Note – A line is a straight path which in practical has no thickness and it can extend in both the directions infinitely. The line segment is a portion of line which is confined between two points, a ray however has an end-point in one direction and extends infinitely in another direction. In all three cases the angles associated is always ${180^0}$.