Answer
467.7k+ views
Hint: When two angles are formed such that they are opposite to each other and intersect at a common point or vertex, then they are called vertically opposite angles and are equal.
The angle formed by a straight line is \[180^\circ\].
Complete step-by-step answer:
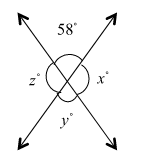
Consider the figure below,
Here the angle \[x\] and \[58^\circ\] lies in a straight line, therefore they are supplementary angles and their sum is equal to \[180^\circ\].
So, the value of angle \[x\] is,
\[x = 180^\circ - 58^\circ = 122^\circ\].
Now, from the figure it is clear that the angles \[58^\circ\] and \[y\] are vertically opposite angles, therefore they are equal.
So, the value of angle \[y\] is,
\[y = 58^\circ\]
Also, angles \[y\] and \[z\] lie in a straight line, therefore they are supplementary angles and their sum is equal to \[180^\circ\].
So, the value of angle \[z\] is,
\[z = 180^\circ - 58^\circ = 122^\circ\].
Therefore, the values of the angles \[x\], \[y\] and \[z\] are \[122^\circ\], \[58^\circ\] and \[122^\circ\] respectively.
Note: You can determine values of the angles using the result that the sum of angles in a complete cycle is \[360^\circ\]. And the sum of angles in a straight line is \[180^\circ\].
The angle formed by a straight line is \[180^\circ\].
Complete step-by-step answer:
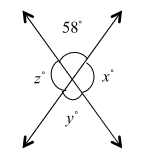
Consider the figure below,

Here the angle \[x\] and \[58^\circ\] lies in a straight line, therefore they are supplementary angles and their sum is equal to \[180^\circ\].
So, the value of angle \[x\] is,
\[x = 180^\circ - 58^\circ = 122^\circ\].
Now, from the figure it is clear that the angles \[58^\circ\] and \[y\] are vertically opposite angles, therefore they are equal.
So, the value of angle \[y\] is,
\[y = 58^\circ\]
Also, angles \[y\] and \[z\] lie in a straight line, therefore they are supplementary angles and their sum is equal to \[180^\circ\].
So, the value of angle \[z\] is,
\[z = 180^\circ - 58^\circ = 122^\circ\].
Therefore, the values of the angles \[x\], \[y\] and \[z\] are \[122^\circ\], \[58^\circ\] and \[122^\circ\] respectively.
Note: You can determine values of the angles using the result that the sum of angles in a complete cycle is \[360^\circ\]. And the sum of angles in a straight line is \[180^\circ\].
Recently Updated Pages
Write the IUPAC name of the given compound class 11 chemistry CBSE

Write the IUPAC name of the given compound class 11 chemistry CBSE

Write the IUPAC name of the given compound class 11 chemistry CBSE

Write the IUPAC name of the given compound class 11 chemistry CBSE

Write the IUPAC name of the given compound class 11 chemistry CBSE

Write the IUPAC name of the given compound class 11 chemistry CBSE

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

How do you graph the function fx 4x class 9 maths CBSE

Which are the Top 10 Largest Countries of the World?

Which is the longest day and shortest night in the class 11 sst CBSE

What is the definite integral of zero a constant b class 12 maths CBSE

Name five important trees found in the tropical evergreen class 10 social studies CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE