Question

Find the volume of a square based right prism whose base is 9 cm and height is 12 cm.

Answer 1

Hint: Find the area of the prism, which is equal to the area of the square. To find the volume, take the product of base area and height.

Complete step-by-step answer:
A square based right prism can also be called a right square prism. It is a box with at least one pair of opposite faces that are square. It can also be desired as a right prism with square bases. A right square prism which has a square lateral surface is a cube.
We can see the figure of a right square prism.

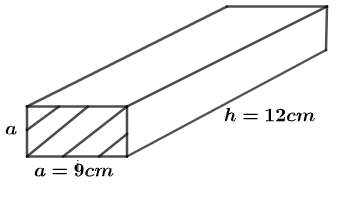
Let us consider ‘a’ as the side of the square. We have been given the side as 9 cm
$\therefore$Side of square $$=a=9\text{cm}$$
Similarly, let us take height as ‘h’ marked in the figure i.e., $$h=12\text{cm}$$.
Now, Area of base of the prism $$=$$ Area of the square $$=$$ $${\left(\text{side}\right)}^{\text{2}}=a^2$$
i.e., Area of the base of the prism $$=a^2=9^2$$
$$=9\times 9=81c{m}^2$$
The volume of right prism $$=\text{Base area}\times \text{height }=a^2\times h$$
$$=81c{m}^2\times h$$
$$=81\times 12=972c{m}^3$$
Hence, we got the volume of the right square prism as $$972c{m}^3$$.

Note: The volume of the right square prism $$=a^{2}h$$, which is a general formula.We can use it directly without thus much calculations. The lateral surface area of the same is given as $$4ah$$.