Question

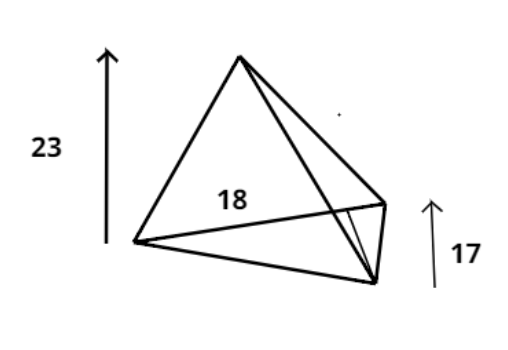
Find the volume of the following triangular pyramid whose base is a triangle with a side of 18 cm and the altitude of 17 cm and the height of the pyramid is 23 cm?

Answer 1

Hint – In this question we have to find the volume of the pyramid given in the question. So use the direct formula to find the volume of the pyramid which is $V = \dfrac{1}{3} \times A \times h$. In order to find the volume first calculate the area of the triangular base. This will help you get the right answer.

“Complete step-by-step answer:”
Given data
Height (h) of pyramid $ = 23$ cm.
The base of the pyramid is a triangle with side length (l) $ = 18$ cm.
And altitude (H) at the side length $ = 17$ cm.
So, as we know that the area (A) of the triangle is half multiplied by side length at which the altitude is time’s altitude.
$ \Rightarrow A = \dfrac{1}{2} \times l \times H$
$ \Rightarrow A = \dfrac{1}{2} \times 18 \times 17 = 9 \times 17 = 153$ Sq. cm.
As we know that the volume (V) of the triangular pyramid is one third multiplied by the area of base time’s height of the pyramid.
$ \Rightarrow V = \dfrac{1}{3} \times A \times h$
\[ \Rightarrow V = \dfrac{1}{3} \times 153 \times 23 = 51 \times 23 = 1173{\text{ c}}{{\text{m}}^3}\]
So, this is the required volume of the pyramid.
So, this is the required answer.

Note – Whenever we face such types of problems the key concept is simply to have the basic understanding of the direct formulae of the volume of the pyramid. We need to keep one thing in mind that the base of the pyramid is composed of a triangular region whose area can be calculated using the formula for the area of the triangle.