Question

Find the volume of the parallelepiped with coterminous edges as $2\hat{i}+3\hat{j}-4\hat{k},5\hat{i}+7\hat{j}+5\hat{k}$ and $4\hat{i}+4\hat{j}-2\hat{k}$

Answer 1

Hint: Use the fact that the area of the parallelogram whose adjacent sides are given by the vectors $\vec{a}$ and $\vec{b}$ is given by $A=\left| \vec{a}\times \vec{b} \right|$. Hence find the area of the base of the parallelepiped. Use the fact that the volume of a parallelepiped with area of base A and height H is given by $V=AH$. Hence determine the volume of the parallelepiped. Alternatively, use the fact that the volume of a parallelepiped with coterminous edges as $\vec{a},\vec{b},\vec{c}$ is given by $V=\left[ \vec{a},\vec{b},\vec{c} \right]$, we have $\left[ \vec{a},\vec{b},\vec{c} \right]$is the scalar triple product of the vectors $\vec{a},\vec{b}$ and $\vec{c}$.

Complete step by step answer:

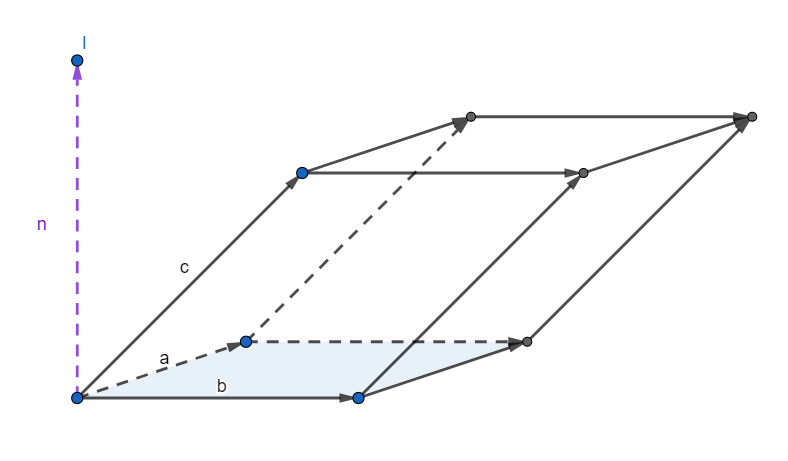
Here $\vec{a}=2\hat{i}+3\hat{j}-4\hat{k},\vec{b}=5\hat{i}+7\hat{j}+5\hat{k}$ and $\vec{c}=4\hat{i}+4\hat{j}-2\hat{k}$
We know that the area of the parallelogram whose adjacent sides are given by the vectors $\vec{a}$ and $\vec{b}$ is given by $A=\left| \vec{a}\times \vec{b} \right|$.
Hence the area of the base of the parallelepiped is given by
\[\begin{align}
  & A=\left| \left( 2\hat{i}+3\hat{j}-4\hat{k} \right)\times \left( 5\hat{i}+7\hat{j}+5\hat{k} \right) \right| \\
 & =\left| 14\hat{k}-10\hat{j}-15\hat{k}+15\hat{i}-20\hat{j}+28\hat{i} \right| \\
 & =\left| 43\hat{i}-30\hat{j}-\hat{k} \right|=\sqrt{{{43}^{2}}+{{30}^{2}}+{{1}^{2}}}=5\sqrt{110} \\
\end{align}\]
Also, the height of the parallelepiped is the projection of $\vec{c}$ on the normal vector of the base of the parallelogram. Note that the normal of the base is the vector $\vec{a}\times \vec{b}$ which as calculated above is given by $\vec{n}=43\hat{i}-30\hat{j}-\hat{k}$
We know that the projection of $\vec{a}$ on $\vec{b}$ is given by $\vec{p}=\dfrac{\vec{a}\cdot \vec{b}}{\left| {\vec{b}} \right|}\hat{b}$
Hence the height of the parallelepiped is given by
$H=\dfrac{\left( 4\hat{i}+4\hat{j}-2\hat{k} \right)\cdot \left( 43\hat{i}-30\hat{j}-\hat{k} \right)}{\sqrt{{{43}^{2}}+{{30}^{2}}+{{1}^{2}}}}=\dfrac{54}{5\sqrt{110}}$
Hence the volume of the parallelepiped is given by
$V=5\sqrt{110}\times \dfrac{54}{5\sqrt{110}}=54$cubic units.

Hence the volume of the parallelepiped is 54 cubic units.

Note: Alternative Solution:
We know that the volume of a parallelepiped with coterminous edges as $\vec{a},\vec{b},\vec{c}$ is given by $V=\left[ \vec{a},\vec{b},\vec{c} \right]$, we have $\left[ \vec{a},\vec{b},\vec{c} \right]$is the scalar triple product of the vectors $\vec{a},\vec{b}$ and $\vec{c}$.
We know that if $\vec{a}={{a}_{1}}\hat{i}+{{a}_{2}}\hat{j}+{{a}_{3}}\hat{k},\vec{b}={{b}_{1}}\hat{i}+{{b}_{2}}\hat{j}+{{b}_{3}}\hat{k},\vec{c}={{c}_{1}}\hat{i}+{{c}_{2}}\hat{j}+{{c}_{3}}\hat{k}$ then
$\left[ \vec{a},\vec{b},\vec{c} \right]=\left| \begin{matrix}
   {{a}_{1}} & {{a}_{2}} & {{a}_{3}} \\
   {{b}_{1}} & {{b}_{2}} & {{b}_{3}} \\
   {{c}_{1}} & {{c}_{2}} & {{c}_{3}} \\
\end{matrix} \right|$
Hence, we have
$\begin{align}
  & V=\left| \begin{matrix}
   2 & 3 & -4 \\
   5 & 7 & 5 \\
   4 & 4 & -2 \\
\end{matrix} \right|=\left| 2\left( -14-20 \right)-3\left( -10-20 \right)-4\left( 20-28 \right) \right| \\
 & =-68+90+32=54 \\
\end{align}$
Which is the same as obtained above.