Question

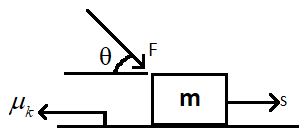
Find the work done by friction for displacement S?

A. ${{\mu }_{k}}\left( mg+F\sin \theta \right)\centerdot S$
B. $-{{\mu }_{k}}\left( mg+F\sin \theta \right)\centerdot S$
C. ${{\mu }_{k}}\left( mg-F\sin \theta \right)\centerdot S$
D. $-{{\mu }_{k}}\left( mg-F\sin \theta \right)\centerdot S$

Answer 1

Hint: In the figure given in the question we are given a block to which a force is applied. Due to the force applied the block gets displaced. To find the work done by friction we need to find the frictional force acting on the block. By finding frictional force and substituting it in the equation for work done, we get the solution.

Formula used:
Frictional force,
$f={{\mu }_{k}}N$
Work done by friction,
$w=-f\times S$

Complete step by step answer:
In the question we are given a block of mass ‘m’.
From the given figure we can see that a force of ‘F’ is acting on the block at an angle of ‘$\theta $’. Due to this force applied on the block, the block gets displaced by ‘S’.
The coefficient of friction between the two surfaces is given as ‘\[{{\mu }_{k}}\]’.
Now let us draw the free body diagram of the given block.

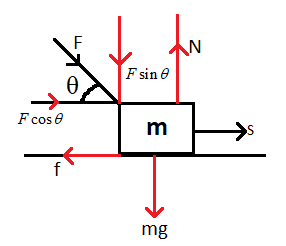
From the figure we can see the forces acting on the block.
Since the force applied to the block is at an angle of ‘$\theta $’, we can resolve the components of the force in x and y directions.
Thus we get ‘$F\sin \theta $’ in the x direction and ‘$F\cos \theta $’ in the y direction.
Therefore the forces acting on the body are: weight of the body acting vertically downwards, Normal force vertically upwards, vertical component of the applied force downwards, horizontal component of the applied force towards right and the frictional force opposite to the direction of motion of the body.
From the figure, we can equate the forces acting on the body as,
$N=F\sin \theta +mg$, where ‘N’ is the normal force, ‘mg’ is the weight of the body and ‘$F\sin \theta $’ is the vertical component of the applied force.
We know that frictional force,
$f={{\mu }_{k}}N$, were ‘$f$’ is frictional force, ‘${{\mu }_{k}}$’ is coefficient of friction, and ‘N’ is the normal force.
We can substitute for normal force here, therefore,
$f={{\mu }_{k}}\left( F\sin \theta +mg \right)$
We need to find the work done by the friction for the displacement ‘S’.
We know that work done by friction,
$w=-f\times S$
By substituting for frictional force, we get
$w=-{{\mu }_{k}}\left( F\sin \theta +mg \right)\centerdot S$
Hence the correct answer is option B.

Note:
For the easy solving of the question we need to construct the free body diagram of the given situation. By drawing a free body diagram we can easily relate the forces acting on the body and the direction of the forces. So in similar questions you should draw the free body diagram of the given body to find the solution.