Question

Find Volume of tetrahedron $\left( {D,ABC} \right)$ where,
$A = \left( { - 4,3,6} \right)$
$B = \left( { - 1,0,3} \right)$
$C = \left( {2,4, - 5} \right)$
$D = \left( {1,1,1} \right)$

Answer 1

Hint: In order to find the volume of the tetrahedron, use the concept of volume of tetrahedron that is given as ($\dfrac{1}{6}th$ of the modulus of the products of the vectors) from which they are formed. Initiate with finding the vectors and then calculate the scalar triple product which would be equal to the determinant of the coefficients of the vectors.

Complete answer: Since, we know that a tetrahedron is a kind of pyramid with a flat polygon base and triangular faces connecting the base to a common point, having four faces, six edges and four vertices. It’s three edges meet at a vertex.
Rough Diagram of tetrahedron is:

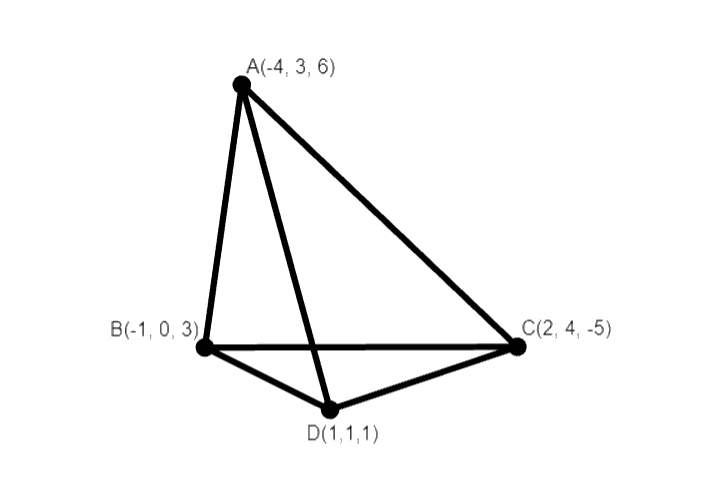
The four vertices given are $D = \left( {1,1,1} \right)$, $A = \left( { - 4,3,6} \right)$, $B = \left( { - 1,0,3} \right)$, $C = \left( {2,4, - 5} \right)$.
Tetrahedron with the given vertices are:

So, the vector $DA$ will be $ = \left( { - 4 - 1} \right)i + \left( {3 - 1} \right)j + \left( {6 - 1} \right)k$, that can be solved and written as $DA = - 5i + 2j + 5k$.
Similarly, vector $DB$ will be $ = \left( { - 1 - 1} \right)i + \left( {0 - 1} \right)j + \left( {3 - 1} \right)k = - 2i - j + 2k$.
And, vector $DC$ will be $ = \left( {2 - 1} \right)i + \left( {4 - 1} \right)j + \left( { - 5 - 1} \right)k = i + 3j - 6k$.

From the formula for the volume of tetrahedron, we know that:
Volume $ = \dfrac{1}{6} \times \left| {scalar\_triple\_product\_of\_these\_three\_vectors} \right|$.
Which can be written as \[Volume = \dfrac{1}{6} \times \left| {\left\{ {\left( {\overrightarrow {DB} \times \overrightarrow {DC} } \right).\overrightarrow {AD} } \right\}} \right|\]
Scalar triple product is written as the determinant of the values of the vectors.
So, it’s written as Scalar triple product \[\left\{ {\left( {\overrightarrow {DB} \times \overrightarrow {DC} } \right).\overrightarrow {AD} } \right\} = \left( {\begin{array}{*{20}{c}}
  { - 5}&2&5 \\
  { - 2}&{ - 1}&2 \\
  1&3&{ - 6}
\end{array}} \right)\]
Solving the matrix determinant, and we get:
\[
  \left( {\begin{array}{*{20}{c}}
  { - 5}&2&5 \\
  { - 2}&{ - 1}&2 \\
  1&3&{ - 6}
\end{array}} \right) \\
   \Rightarrow - 5\left( {\left( { - 1 \times - 6} \right) - \left( {3 \times 2} \right)} \right) - 2\left( {\left( { - 2 \times - 6} \right) - \left( {1 \times 2} \right)} \right) + 5\left( {\left( { - 2 \times 3} \right) - \left( { - 1 \times 1} \right)} \right) \\
 \]
Solving the inner and outer parenthesis, and we get:
\[
   \Rightarrow - 5\left( {\left( 6 \right) - \left( 6 \right)} \right) - 2\left( {\left( {12} \right) - \left( 2 \right)} \right) + 5\left( {\left( { - 6} \right) + 1} \right) \\
   \Rightarrow - 5\left( 0 \right) - 2\left( {10} \right) + 5\left( { - 5} \right) \\
   \Rightarrow 0 - 20 - 25 \\
   \Rightarrow - 45 \\
 \]

Therefore, the scalar triple product value is \[\left\{ {\left( {\overrightarrow {DB} \times \overrightarrow {DC} } \right).\overrightarrow {AD} } \right\} = - 45\].
Substituting this value in the volume, and we get:
\[Volume = \dfrac{1}{6} \times \left| { - 45} \right|\]
Solving the modulus:
\[Volume = \dfrac{{45}}{6}\]
Since, the value can be further simplified in simplified fractions and can be written as \[\dfrac{{45}}{6} = \dfrac{{15}}{2}\], so the volume of the tetrahedron is \[\dfrac{{15}}{2}\] units.

Note:
Since, volume is a positive quantity so always apply modulus to the scalar product.
In the case of a tetrahedron if the base is a triangle with any four faces that can be considered as the base, because of which a tetrahedron is also known as a triangular pyramid.