
How do you find which quadrant each question is referring to if
Answer
463.8k+ views
Hint: We explain the central angle around a point. Then we discuss the algebraic and geometric versions of the quadrants. We also find different quadrants and their characteristics. Then we find the solutions for the angles
Complete step by step answer:
The central angle around a point is always equal to
The total angle is divided into four parts or quadrant as they are called. These quadrants are named in roman numerals of
In case of algebraic sense these quadrants give the signs of the x and y coordinates.
These quadrants are also called as the first, second, third and fourth quadrant.
The respective signs for the coordinates of
Now we look for the geometric side of the quadrants where we deal with the angle of the trigonometric ratios.
The total circular angle of
Therefore, the first quadrant is the interval of
Now we find for the quadrants
When the angle
Note:
We can also represent the quadrants with respect to the image form of both algebraic and geometric versions.
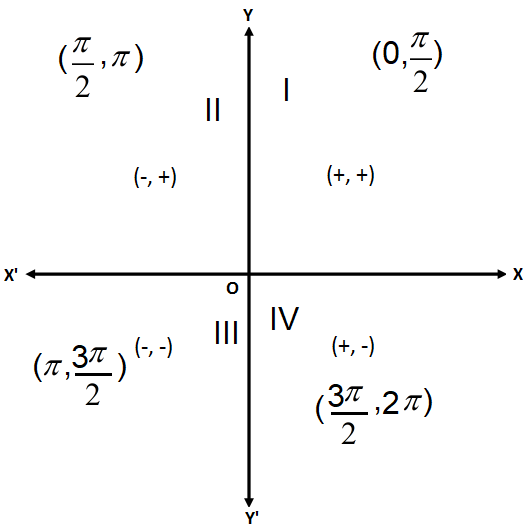
The rotation of the coordinates happens anti-clockwise.
Complete step by step answer:
The central angle around a point is always equal to
The total angle is divided into four parts or quadrant as they are called. These quadrants are named in roman numerals of
In case of algebraic sense these quadrants give the signs of the x and y coordinates.
These quadrants are also called as the first, second, third and fourth quadrant.
The respective signs for the coordinates of
Now we look for the geometric side of the quadrants where we deal with the angle of the trigonometric ratios.
The total circular angle of
Therefore, the first quadrant is the interval of
Now we find for the quadrants
When the angle
Note:
We can also represent the quadrants with respect to the image form of both algebraic and geometric versions.
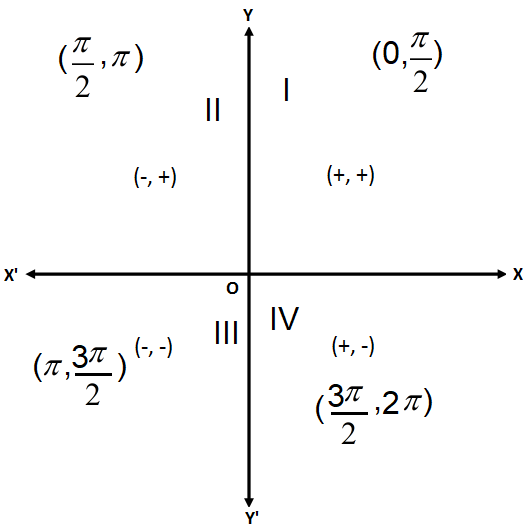
The rotation of the coordinates happens anti-clockwise.
Latest Vedantu courses for you
Grade 10 | CBSE | SCHOOL | English
Vedantu 10 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹37,300 per year
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




