
Find work done by frictional force in B by A during the displacement:
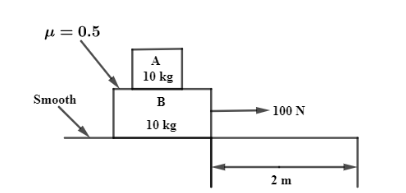
(a).
(b).
(c).
(d).

Answer
510.6k+ views
Hint: First of all, we will calculate limiting frictional force by B on A and then we will find frictional force needed to move along with B if both are same then using its value we will find work done by using the formula
Formula used:
Complete step by step answer:
Now, as shown in figure in the question, we know that
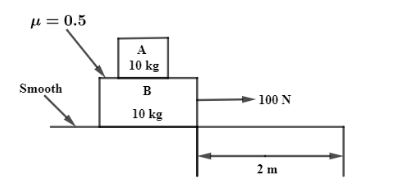
First of all, we will denote
Now, we know that the force P acts in positive direction so due to that frictional force always acts in direction opposite to it. So, the limiting frictional force by B on A will be in the opposite direction. The limiting frictional force is given by,
Now, as the frictional force acts on object A here mass will be
Now, the value of
Hence, the limiting force is 50 N and as it acts in the opposite direction it will be
Now, we know that frictional force on mass 2 by mass 1 can be given by,
Now, we will substitute the values in this equation and then we will get
Hence, the frictional force needed is also 50 N. As, limiting and frictional forces are same we will consider any one of them as force needed to drag and find the work done using formula,
Hence, work done is 100 J and as the frictional force is in the opposite direction the work done by that force will be
Thus, option (b) is correct.
Note: In this type of question, students must understand that here limiting and frictional forces are the same but if they are different in value then we have to take their difference to find the final force acting and in which direction it acts. The direction of force and frictional force should always be in opposite directions, students might take them in the same direction and then the answer will be wrong.
Formula used:
Complete step by step answer:
Now, as shown in figure in the question, we know that

First of all, we will denote
Now, we know that the force P acts in positive direction so due to that frictional force always acts in direction opposite to it. So, the limiting frictional force by B on A will be in the opposite direction. The limiting frictional force is given by,
Now, as the frictional force acts on object A here mass will be
Now, the value of
Hence, the limiting force is 50 N and as it acts in the opposite direction it will be
Now, we know that frictional force on mass 2 by mass 1 can be given by,
Now, we will substitute the values in this equation and then we will get
Hence, the frictional force needed is also 50 N. As, limiting and frictional forces are same we will consider any one of them as force needed to drag and find the work done using formula,
Hence, work done is 100 J and as the frictional force is in the opposite direction the work done by that force will be
Thus, option (b) is correct.
Note: In this type of question, students must understand that here limiting and frictional forces are the same but if they are different in value then we have to take their difference to find the final force acting and in which direction it acts. The direction of force and frictional force should always be in opposite directions, students might take them in the same direction and then the answer will be wrong.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




