Question

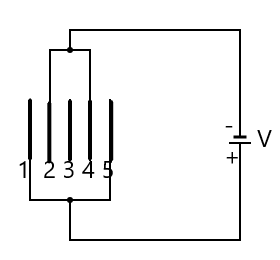
Five identical plates each of area $A$ are joined as shown in the figure. The distance between the plates is $d$. The plates are connected to a potential difference of $V$ volts. The charge in plate 2 and 4 will be:

(A) ${\varepsilon _0}\dfrac{{AV}}{d},2{\varepsilon _0}\dfrac{{AV}}{d}$
(B) ${\varepsilon _0}\dfrac{{AV}}{d},2{\varepsilon _0}\dfrac{{AV}}{d}$
(C) ${\varepsilon _0}\dfrac{{AV}}{d}, - 2{\varepsilon _0}\dfrac{{AV}}{d}$
(D) $ - {\varepsilon _0}\dfrac{{AV}}{d}, - {\varepsilon _0}\dfrac{{AV}}{d}$

Answer 1

Hint Any two plates close enough to each other containing opposite charges can be considered a capacitor. A capacitor has one plate of negative charge and another of positive charge. Now using the formula for the charge of a capacitor plate, we can calculate the charge on the given plate.
Formula used: In this solution we will be using the following formulae;
$\Rightarrow Q = CV$ where $Q$ is the amount of charge on a plate of a capacitor, $C$ is the capacitance of the capacitor, and $V$ is the potential difference across the two plates.
$\Rightarrow C = {\varepsilon _0}\dfrac{A}{d}$ where $C$ is the capacitance of the capacitor, ${\varepsilon _0}$ is the permittivity of free space, $A$ is the area of the plates, and $d$ is the distance between the plates.

Complete step by step answer
A capacitor can simply be considered as two plates placed at close proximity to each other. When these plates are connected to a cell or battery they can be used to store charges. Each plate stores equal and opposite charges based on which terminal of the cell was connected to the capacitor. The plate connected to the negative terminal store negative charges, the plate connected to the terminal store positive charges.
From the diagram, we can see that plate 1 and 2 can be regarded as the plates of a capacitor. The charge on one of the plates of a capacitor is given as
$\Rightarrow Q = CV$ where $C$ is the capacitance of the capacitor, and $V$ is the potential difference across the two plates.
But the capacitance is given as
$\Rightarrow C = {\varepsilon _0}\dfrac{A}{d}$ where ${\varepsilon _0}$ is the permittivity of free space, $A$ is the area of the plates, and $d$ is the distance between the plates.
Hence, by replacing $C$ in $Q = CV$ we have
$\Rightarrow Q = {\varepsilon _0}\dfrac{A}{d}V$.
Now since we are interested in the charge in plate 2, we must note that the terminal of the cell connected to the plate is negative, thus the charge in plate 2 is negative.
Hence
$\Rightarrow {Q_2} = - {\varepsilon _0}\dfrac{A}{d}V$ where ${Q_2}$ signifies charge in plate 2.
Similarly, plate 4 and 5 also constitute a capacitor,
Hence, the charge in each plate is also equal to
$\Rightarrow Q = {\varepsilon _0}\dfrac{A}{d}V$
The plate 4 is also connected to the negative charge of the terminal hence
$\Rightarrow {Q_4} = - {\varepsilon _0}\dfrac{A}{d}V$
Thus, option D is the answer.

Note
The plate 3 does not affect the charges in any of the plates of the capacitors. This is because it is isolated and not connected to any of the terminals, thus has no charge contained in itself to play any part.