Question

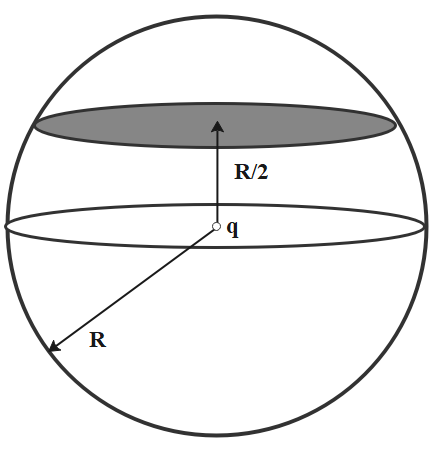
Flux passing through the shaded surface of a sphere when a point charge q is placed at the centre is (Radius of the sphere is R):

 (A)$\dfrac{q}{{{\varepsilon }_{0}}}$
(B)$\dfrac{q}{2{{\varepsilon }_{0}}}$
(C)$\dfrac{q}{4{{\varepsilon }_{0}}}$
(D)Zero

Answer 1

Hint: The flux flowing through both the regions that are marked will be the same since the charge is placed at the centre of the sphere and electric field lines from the charge spread out in the radial direction. Applying this concept, we try to solve this problem.
Formula Used:
The electric flux is given by, $\phi $ =E.dA

Complete answer:
Since the charge is placed at the centre of the sphere, the electric field directs all over the sphere in radial direction. The property of electric field lines that they do not intersect with each other explains the fact that the two regions that are marked have the same flux flowing through them, that is the flux in the top and bottom regions are the same.
Let us consider a small surface element on the surface that subtends an angle $d\theta $and$d\phi $.
The area is given in spherical coordinates as follows:
dA = ${{R}^{2}}\sin \theta d\theta d\phi \text{ }\hat{r}$
The flux is given by d$\phi $ = E. dA
 $\Rightarrow d\phi =\dfrac{q}{4\pi {{\varepsilon }_{0}}{{R}^{2}}}{{R}^{2}}\sin \theta d\theta d\phi $
The value $\theta $ from 0 to $\dfrac{\pi }{3}$ and $\phi $ varies from 0 to 2$\pi $ .
Therefore, the flux is given as
$\phi =\iint{\dfrac{q}{4\pi {{\varepsilon }_{0}}}}\sin \theta d\theta d\phi $
Taking the limit over the integral, we have
$\phi =\dfrac{q}{4{{\varepsilon }_{0}}}$
Thus the value of flux for the shaded region given in the figure below is $\dfrac{q}{4{{\varepsilon }_{0}}}$.

Hence the correct option is (C) $\dfrac{q}{4{{\varepsilon }_{0}}}$.

Additional Information:
Electric flux is the rate of flow of electric field through a given area. Electric flux can be said to be directly proportional to the number of lines entering the surface. In fact flux gives us a description of electric field strength at any distance from the charge causing the field.

Note:
The charge is placed at the centre of the sphere so we must consider the radial direction of the electric field while calculating the flux. Also we need to properly define the integration limits as any slight mistake will create errors in the entire problem at hand.