Question

For a common emitter configuration, if $\alpha $ and $\beta $ have their usual meaning the correct relationship between $\alpha $ and $\beta $ is:
A. $\dfrac{1}{\alpha }=\dfrac{1}{\beta }+1$
B. $\alpha =\dfrac{\beta }{1-\beta }$
C. $\alpha =\dfrac{\beta }{1+\beta }$
D. $\alpha =\dfrac{{{\beta }^{2}}}{1-{{\beta }^{2}}}$

Answer 1

Hint: Common emitter is the configuration of an amplifier. The circuit is assembled in such a way that the emitter is connected between the collector and the base of the amplifier. This emitter is common to both the input and the output of the circuit. The amplifier is also known as a bipolar junction transistor that is used to amplify the input current.

Complete step by step answer:
The common emitter configuration can be understood with more clarity from the diagram given here,

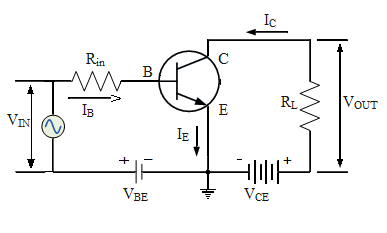
In this type of circuit the current thought the circuit is the sum of the current coming from the collector and the base.
Mathematically,
${{I}_{E}}={{I}_{B}}+{{I}_{C}}$
The ratio of the input base current and the collector current is known as the current gain denoted by$\beta $.
$\dfrac{{{I}_{C}}}{{{I}_{B}}}=\beta $
The current gain of the common emitter amplifier is large.
The ratio of the collector current and the emitter current is known as alpha symbolically represented as $\alpha $
$\dfrac{{{I}_{C}}}{{{I}_{E}}}=\alpha $
From the current gain, the collector current can be written as,
${{I}_{C}}={{I}_{E}}\beta $
By putting the values of the emitter current and collector current in alpha
\[\begin{align}
  & \dfrac{\beta {{I}_{B}}}{{{I}_{C}}+{{I}_{B}}}=\alpha \\
 & \Rightarrow \dfrac{1}{\alpha }=\dfrac{{{I}_{C}}}{\beta {{I}_{B}}}+\dfrac{{{I}_{B}}}{\beta {{I}_{B}}} \\
\end{align}\]
The ratio of collector current and emitter current is given as $\dfrac{{{I}_{C}}}{{{I}_{B}}}=\beta $
So,
$\dfrac{1}{\alpha }=1+\dfrac{1}{\beta }$
This can be rearranged as,
$\alpha =\dfrac{1+\beta }{\beta }$
This is the relationship between the two terms $\alpha $ and $\beta $.

So, the correct answer is “Option A”.

Note: The output impedance of the CE (common-emitter) amplifier is very high whereas the input impedance of the CE configuration circuit is quite low. When we consider the power gain of such amplifiers it seems to be very high. These parameters are estimated by the current flowing through the collector, base, and emitter and the voltage supplied to the circuit.