Question

For a second order, the graph plotted between ${{[A]}^{-1}}$and time ‘t’ is shown here. $\theta ={{\tan }^{-1}}(0.5)$ and OP = $2Lmo{{l}^{-1}}$. Thus, rate of the reaction at start is:

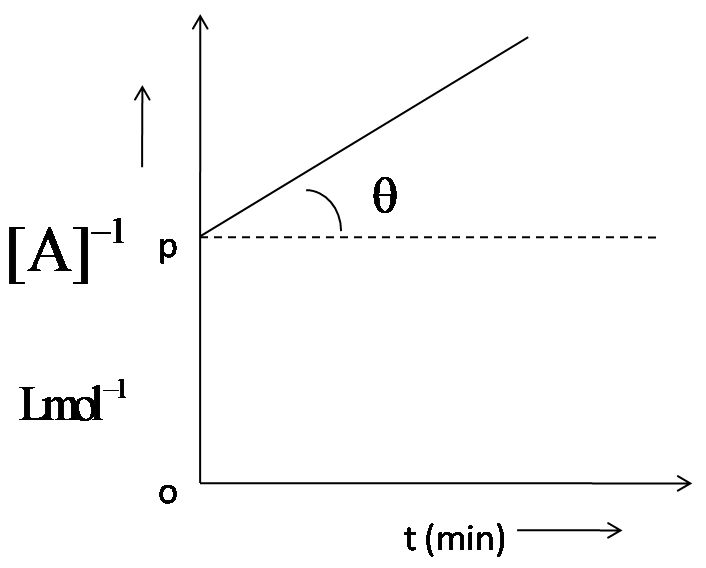
A.$125\,Lmo{{l}^{-1}}{{\min }^{-1}}$
B.$0.124\,Lmo{{l}^{-1}}{{\min }^{-1}}$
C.$1.25\,mol\,Lmo{{l}^{-1}}{{\min }^{-1}}$
D.$0.5\,mol\,Lmo{{l}^{-1}}{{\min }^{-1}}$

Answer 1

Hint: The reaction in which the concentration of the species that are reacting is raised to the power of two is the second order reaction. Rate constant of any reaction is the relationship between concentration of the reactants and the rate. Rate constant of the second order reaction has unit $mo{{l}^{-1}}L{{\sec }^{-1}}$.

Complete answer:
We have been given a graph plotted between $\dfrac{1}{[A]}$ and time ‘t’. It is a second order reaction. We have to determine the rate of the reaction at the start.
So, For this second order reaction (involving one reactant A), the equation will be $2A\to products$. Applying the law of mass action, the rate of this reaction will be, $\dfrac{dx}{dt}\propto {{[A]}^{2}}$
So, changing the proportionality with rate constant k, we have,
$\dfrac{dx}{dt}=k{{[A]}^{2}}$, this equation can be rewritten as,
$\dfrac{dx}{{{[A]}^{2}}}=kdt$
Integrating the above equation we have,
$\int{\dfrac{dx}{{{[A]}^{2}}}=\int{kdt}}$ this will be,
$\dfrac{{{[A]}^{-1}}}{-1}\times (-1)=kt+I$
$\dfrac{1}{{{[A]}^{-1}}}=kt+I$ , where $I$ is the constant of integration. In the beginning, time, t = 0, and the reactant will be A only, as it has not been reacted.
This equation resembles the equation of a line, slope- intercept form, which is y = mx + b, where m is the slope, x is the x coordinate, y is the y coordinate, and b is the y intercept.
The second order reaction has led to $\dfrac{1}{{{[A]}^{-1}}}=kt+I$, from which it is clear that the slope of the graph gives us rate constant, while y coordinate gives $\dfrac{1}{[A]}$and x coordinate time, ‘t’. so, the slope of the straight line which is $\tan \theta $ will give us the rate. As given, $\theta ={{\tan }^{-1}}=0.5$, this will be the rate of the reaction.

Hence, the rate of the reaction at the start is $0.5\,mol\,Lmo{{l}^{-1}}{{\min }^{-1}}$, so option D is correct.

Note:
The derivation explained is the integrated form of rate equation, rate equation states that rate is directly proportional to the concentration of reactants. Through the integration of rate equation for second order reaction, we can obtain the slope- intercept form equation, which can tell us the value of rate constant, which is the slope of the graph between concentration and time.