Question

For some non-zero vector \[\overrightarrow V \], if the sum of \[\overrightarrow V \] and the vector obtained from \[\overrightarrow V \] by rotating it by an angle \[2\alpha \] equals to the vector obtained from \[\overrightarrow V \] by rotating it by a then the value of \[\alpha \], is where \[n\] is a integer.
A.\[2n\pi = \dfrac{\pi }{3}\]
B.\[n\pi = \dfrac{\pi }{3}\]
C.\[2n\pi = \dfrac{{2\pi }}{3}\]
D.\[n\pi = \dfrac{{2\pi }}{3}\]

Answer 1

Hint: In this problem, A nonzero vector is a vector with magnitude not equal to zero. The vector obtained by rotating the vector \[\overrightarrow V \] by an angle \[\alpha \] in the anticlockwise direction is defined by trigonometric formula. A vector is an object that has both a magnitude and a direction.

Complete step-by-step answer:

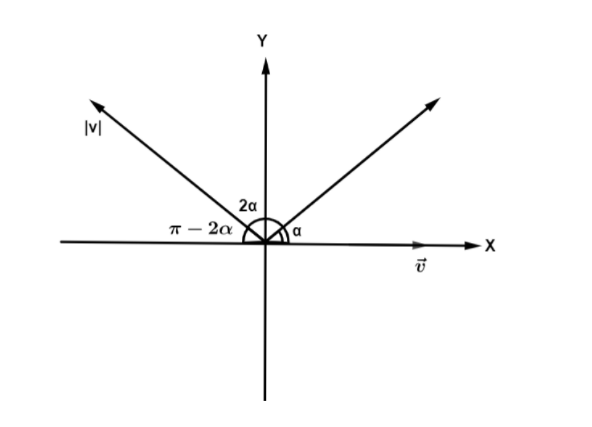
First, we have to sketch a diagram for some non-zero vector \[\overrightarrow V \], if the sum of \[\overrightarrow V \] and the vector obtained from \[\overrightarrow V \] by rotating it by an angle \[2\alpha \] equals to the vector obtained from \[\overrightarrow V \] by rotating it by a then the value of \[\alpha \], is where \[n\] is a integer.
According to the condition in this problem, the vector obtained by rotating the vector \[\overrightarrow V \] by an angle\[\alpha \] in the anticlockwise direction, then
\[vi - v\cos (\pi - 2\alpha )\hat i + v\sin (\pi - 2\alpha )\hat j = v\cos \alpha \hat i + v\sin \alpha \hat j\]
We use the trigonometric identity $\cos (\pi - \theta ) = - \cos \theta $ and $\sin (\pi - \theta ) = \sin \theta $, we can get
Since, $\cos (\pi - 2\alpha ) = - \cos 2\alpha $ and $\sin (\pi - 2\alpha ) = \sin 2\alpha $
\[v\hat i - v( - cos2\alpha \hat i) + v\sin 2\alpha \hat j = v\cos \alpha \hat i + v\sin \alpha \hat j\],
\[v\hat i + vcos2\alpha \hat i + v\sin 2\alpha \hat j = v\cos \alpha \hat i + v\sin \alpha \hat j\]
Put common factor ‘v’ from bracket, we have
\[v(1 + cos2\alpha )\hat i + v\sin 2\alpha \hat j = v\cos \alpha \hat i + v\sin \alpha \hat j\]
On separating i and j part on both sides of the equation, then
\[v(1 + \cos 2\alpha ) = v\cos \alpha \] and $v\sin 2\alpha = v\sin \alpha $
By dividing on both sides by ‘v’, we get
\[(1 + \cos 2\alpha ) = \cos \alpha \] and $\sin 2\alpha = \sin \alpha $
Here, by using this trigonometric identity , $\cos 2\alpha = 2{\cos ^2}\alpha - 1$ and $2\sin \alpha \cos \alpha = \sin \alpha $
\[1 + 2{\cos ^2}\alpha - 1 = \cos \alpha \] and $2\sin \alpha \cos \alpha = \sin \alpha $
On further simplification, we get
\[2{\cos ^2}\alpha = \cos \alpha \] and $2\cos \alpha = 1$
\[2{\cos ^2}\alpha - \cos \alpha = 0\] and \[\cos \alpha = \dfrac{1}{2}\]
Take out \[\cos \alpha \] commonly on the first function, then
\[\cos \alpha (2\cos \alpha - 1) = 0\] and \[\cos \alpha = \dfrac{1}{2}\]
Separate the factors to find the value of , then
\[\cos \alpha = 0\], \[(2\cos \alpha - 1) = 0\] and \[\cos \alpha = \dfrac{1}{2}\]
Expanding the equation from LHS to RHS, then
\[\cos \alpha = 0\], \[2\cos \alpha = 1 \Rightarrow \cos \alpha = \dfrac{1}{2}\] and \[\cos \alpha = \dfrac{1}{2}\]
\[\cos \alpha = 0\],\[\cos \alpha = \dfrac{1}{2}\] and $\cos \alpha = \dfrac{1}{2}$
We know that, the formula $\cos \dfrac{\pi }{2} = 0 \Rightarrow \alpha = 2n\pi \pm \dfrac{\pi }{2}$ and $\cos \dfrac{\pi }{3} = \dfrac{1}{2} \Rightarrow \alpha = 2n\pi \pm \dfrac{\pi }{3}$,
$\alpha = 2n\pi \pm \dfrac{\pi }{2}$, $\alpha = 2n\pi \pm \dfrac{\pi }{3}$ and $\alpha = 2n\pi \pm \dfrac{\pi }{3}$
Therefore, $\alpha = 2n\pi \pm \dfrac{\pi }{3}$ satisfies both equations.
Hence, The final answer is option(A) \[2n\pi = \dfrac{\pi }{3}\]
So, the correct answer is “Option A”.

Note: Geometrically, we can define a vector as a directed line segment, whose length is the magnitude of the vector and with an arrow indicating the direction. The direction of the vector is from its tail to its head.