Question

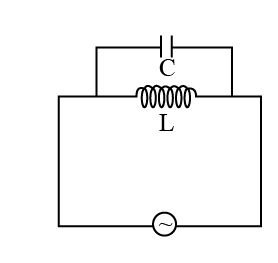
For the circuit shown in the figure the current through the inductor is 1.6 A, while the current through the condenser is 0.4 A, then the current I drawn from the source is,

A. \[2\sqrt 2 \;{\rm{A}}\]
B. \[1.65\;{\rm{A}}\]
C. \[1.2\;{\rm{A}}\]
D. \[2.0\;{\rm{A}}\]

Answer 1

Hint: The above problem can be resolved using the concepts and fundamental relations for the phase difference on the voltage supply as well as the current flow across the given capacitive- Inductive circuit. Moreover, this phase difference will decide the idea of the required current flow from the given source.


Complete step-by-step solution:
Given:
The magnitude of current through the inductor is, \[{I_1} = 1.6\;{\rm{A}}\].
 The magnitude of current through the condenser is, \[{I_2} = 0.4\;{\rm{A}}\].
 The circuit consisting of capacitor capacitance C and inductor of inductance L is shown in the figure,
Let I be the current drawn from the source
In an L-C circuit, the capacitor possesses a lead of \[90\;^\circ \]in its voltage supply, while the inductor possesses the lag of \[90\;^\circ \] in its voltage supply. This account for the current flow through the inductor will lag by \[180\;^\circ \] with respect to the current flow across the capacitor or the condenser.
Then the magnitude of current drawn from the source is given as,
\[I = {I_1} - {I_2}\]
Substituting the values,
\[\begin{array}{l}
I = {I_1} - {I_2}\\
I = 1.6\;{\rm{A}} - 0.4\;{\rm{A}}\\
I = 1.2\;{\rm{A}}
\end{array}\]
Therefore, the required magnitude of current from the source is 1.2 A and option C is correct.


Note: The problem uses the concepts of phase difference among the voltages, therefore it is important to remember the phase differences for the various kinds of circuits like LC circuit, RL circuit, RLC circuit and many more. Along with this the key concept of the phases of current flow is also to be remembered to resolve the given condition.