Question

For the damped oscillator shown in Fig, the mass of the block is $200g$, $k=80\text{N}{\text{m}}^{-1}$ and the damping constant b is $40\text{g}{\text{s}}^{-1}$.

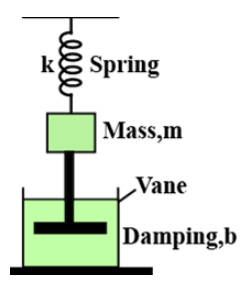
Calculate:
(a) The period of oscillation,
(b) Time period for its amplitude of vibrations to drop to half of its initial value
(c) The time for the mechanical energy to drop to half initial value.

Answer 1

Hint: The amplitude of oscillations steadily decreases over time as a result of radiation from an oscillating mechanism and friction in the system. An oscillator's amplitude (or energy) is reduced by damping, and the oscillations are said to be damped.

Complete step by step answer:
Damping is a force acting inside or on an oscillatory organ that reduces or prevents it from oscillating. Damping is created in physical systems by processes that dissipate the energy contained in the oscillation. Viscous drag in mechanical devices, resistance in electronic oscillators, and light absorption and scattering in optical oscillators are all examples. Other oscillating mechanisms, such as those used in biological systems and bicycles, may benefit from damping that is not dependent on energy loss.

(a) $$\begin{gathered} {\displaystyle \frac{\text{k}}{\text{m}}}={\displaystyle \frac{90}{0.2}} \\ \Rightarrow {\displaystyle \frac{\text{k}}{\text{m}}}=450\text{N}{\text{m}}^{-1}\text{k}{\text{g}}^{-1} \end{gathered}$$
$\Rightarrow {\displaystyle \frac{{\text{b}}^2}{4{\text{m}}^2}}={\displaystyle \frac{{(0.04)}^2}{4\times {(0.2)}^2}}=0.01\text{k}{\text{g}}^2{\text{s}}^{-2}$
$\text{ As, }{\displaystyle \frac{\text{k}}{\text{m}}}\gg >{\displaystyle \frac{{\text{b}}^2}{4{\text{m}}^2}},\text{ therefore, }$
$\Rightarrow {\omega }^{\prime }=\sqrt{{\displaystyle \frac{k}{m}}-{\displaystyle \frac{b^2}{4m^2}}}\approx \sqrt{{\displaystyle \frac{k}{m}}}$
$\Rightarrow \text{T}={\displaystyle \frac{2\pi }{{\omega }^{\prime }}}=2\pi \sqrt{{\displaystyle \frac{\text{m}}{\text{k}}}}$
$\Rightarrow \text{T}=2\times {\displaystyle \frac{22}{7}}\sqrt{{\displaystyle \frac{0.2}{90}}}\approx 0.3\text{s}$
$\therefore T=0.3s$

(b) If $T$ is the time when the amplitude of the damped oscillations decreases to half its original value, then the amplitude of the damped oscillations at time t is
$a=x_0{e}^{-bT/2m}$
$\text{ when }t=T,a=x_0/2$
${\displaystyle \frac{x_0}{2}}=x_0{e}^{-bT/2m}$
$\text{ or }2=e^{bT/2m}\text{ or }{\log }_{e}2={\displaystyle \frac{bT}{2m}}$
$\Rightarrow \text{T}={\displaystyle \frac{2\text{m}}{\text{b}}}{\log }_{\text{e}}2$
$\Rightarrow T={\displaystyle \frac{2.3026\times 2\text{m}}{\text{b}}}{\log }_{10}2$
$\Rightarrow T={\displaystyle \frac{2.3026\times 2\times 0.2\times 0.3010}{0.04}}$
$\therefore T=6.93\text{s}$

(c) If T’ is the time, when mechanical energy drops to half its mechanical energy$E_o$, then mechanical energy E of the damped oscillations at an instant t is given by
$\text{E}={\text{E}}_0{\text{e}}^{-\text{bt}/\text{m}}$
$\text{ When }t=T^{\prime },E=E_0/2\text{ then }{\displaystyle \frac{E_0}{2}}=E_0{e}^{-bT/m}$
$\Rightarrow 2={\text{e}}^{\text{b}{\text{T}}^{‘}/\text{m}}$
$\Rightarrow {\log }_{\text{e}}2={\displaystyle \frac{\text{b}{\text{T}}^{\prime }}{\text{m}}}$
$\Rightarrow {\text{T}}^{\prime }=2.3026{\log }_{10}2\times {\displaystyle \frac{\text{m}}{\text{b}}}$
$\Rightarrow {\text{T}}^{\prime }=2.3026\times 0.3010\times {\displaystyle \frac{0.2}{0.04}}$
$\therefore T^{\prime }=3.46\text{s}$

Note: The period and frequency of a device with a small amount of damping are approximately the same as with basic harmonic motion, but the amplitude steadily decreases. Since the non-conservative damping force extracts energy from the device, usually in the form of thermal energy, this happens.