
For the line parallel to the x-axis
Points and Coordinate A B C D x 1 4 3 6 y 2 2 2 2 (x, y) (1, 2) (4, 2) (3, 2) (6, 2)
For the line parallel to the y-axis
Points and Coordinate P Q R S x 1 1 1 1 y 2 0 4 3 (x, y) (1, 2) (1, 0) (1, 4) (1, 3)
(i) In the table for the line parallel to the x-axis for any value of x, y is always ________.
(ii) In the table for the line parallel to the y-axis for any value of y, x is always ________.
(iii) So, the equation of line parallel to the x – axis is y = __________ it can also be written as 0x + y = ______.
(iv) So, the equation of line parallel to the y – axis is x = __________ it can also be written as x + 0y = ______.
| Points and Coordinate | A | B | C | D |
| x | 1 | 4 | 3 | 6 |
| y | 2 | 2 | 2 | 2 |
| (x, y) | (1, 2) | (4, 2) | (3, 2) | (6, 2) |
| Points and Coordinate | P | Q | R | S |
| x | 1 | 1 | 1 | 1 |
| y | 2 | 0 | 4 | 3 |
| (x, y) | (1, 2) | (1, 0) | (1, 4) | (1, 3) |
Answer
564.9k+ views
Hint: To solve this question, we will first make the graph of both the tables separately using the coordinates given below each table and then try to answer the question given above. Also, from that, we will calculate the equation of line as well.
Complete step-by-step solution
Let us consider the first table. For the line parallel to the x-axis.
Let us draw the given coordinates in the below graph of the x and y-axis.
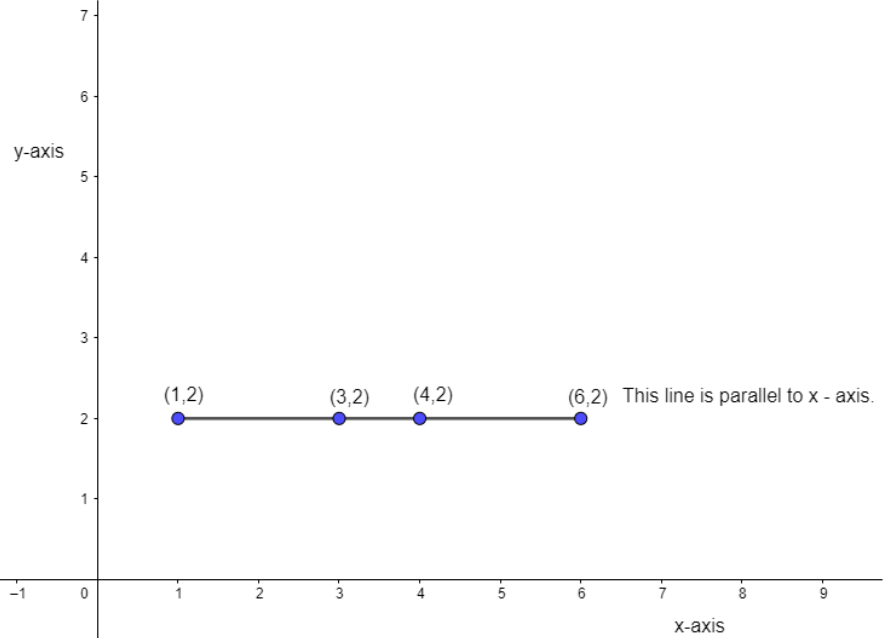
Sol let us answer part (i).
(i) In the table for the line parallel to the x-axis for any value of x, y is always constant. As the graph shows a line parallel to the x-axis. Hence, the line parallel to the x-axis has all the values of y as constant.
Let us answer part (iii).
(iii) The equation of line parallel to the x-axis is y = 2 as for all values of x, y = 2. It can also be written as
\[0x+y\]
\[\Rightarrow 0x+2\]
\[\Rightarrow 2\]
Hence, the answer of (iii) is $0x+2$
So, the equation of line parallel to the x-axis is y = 2 it can also be written as 0x + y = 2.
Now let us consider the second table, the line parallel to the y-axis.
Let us draw the given coordinates in the below graph of the x and y-axis.
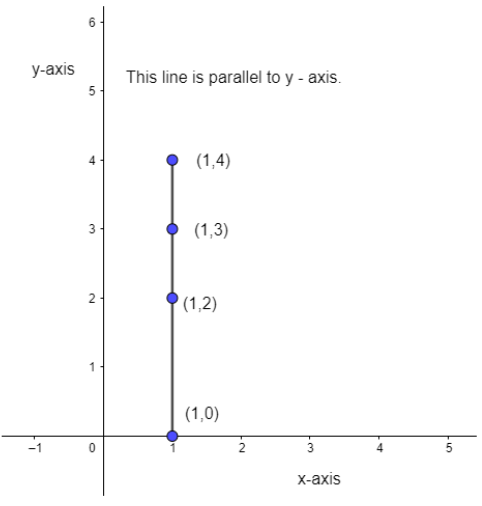
So, we observe that we have made the graph and it is a line parallel to the y-axis. Let us answer part (ii) now.
(ii) In the table for the line parallel to the y-axis for any value of y, x is always constant. This is so as we see that for $y = 0, x = 1; y = 2, x = 1 y = 4; x = 1; y = 3, x = 1.$
Hence, the line parallel to the y-axis has all the values of x as constant.
Let us answer part (iv) now.
(iv) So, the equation of line parallel to y – axis is x = 1 it can also be written as x + 0y = 1.
\[\Rightarrow x+0y\]
\[\Rightarrow x=1\]
\[\Rightarrow x+0y=1\]
Hence, all parts (i), (ii), (iii), and (iv) are answered.
Note: A line which has coordinates of y fixed is a line parallel to the x-axis as any be the value of x the y – coordinate is fixed. Similarly, it is the case when a line having coordinate of x-axis fixed is a line parallel to y-axis as any be the value of y the x coordinate is fixed.
Complete step-by-step solution
Let us consider the first table. For the line parallel to the x-axis.
| Points and Coordinate | A | B | C | D |
| x | 1 | 4 | 3 | 6 |
| y | 2 | 2 | 2 | 2 |
Let us draw the given coordinates in the below graph of the x and y-axis.

Sol let us answer part (i).
(i) In the table for the line parallel to the x-axis for any value of x, y is always constant. As the graph shows a line parallel to the x-axis. Hence, the line parallel to the x-axis has all the values of y as constant.
Let us answer part (iii).
(iii) The equation of line parallel to the x-axis is y = 2 as for all values of x, y = 2. It can also be written as
\[0x+y\]
\[\Rightarrow 0x+2\]
\[\Rightarrow 2\]
Hence, the answer of (iii) is $0x+2$
So, the equation of line parallel to the x-axis is y = 2 it can also be written as 0x + y = 2.
Now let us consider the second table, the line parallel to the y-axis.
| Points and Coordinate | P | Q | R | S |
| x | 1 | 1 | 1 | 1 |
| y | 2 | 0 | 4 | 3 |
Let us draw the given coordinates in the below graph of the x and y-axis.

So, we observe that we have made the graph and it is a line parallel to the y-axis. Let us answer part (ii) now.
(ii) In the table for the line parallel to the y-axis for any value of y, x is always constant. This is so as we see that for $y = 0, x = 1; y = 2, x = 1 y = 4; x = 1; y = 3, x = 1.$
Hence, the line parallel to the y-axis has all the values of x as constant.
Let us answer part (iv) now.
(iv) So, the equation of line parallel to y – axis is x = 1 it can also be written as x + 0y = 1.
\[\Rightarrow x+0y\]
\[\Rightarrow x=1\]
\[\Rightarrow x+0y=1\]
Hence, all parts (i), (ii), (iii), and (iv) are answered.
Note: A line which has coordinates of y fixed is a line parallel to the x-axis as any be the value of x the y – coordinate is fixed. Similarly, it is the case when a line having coordinate of x-axis fixed is a line parallel to y-axis as any be the value of y the x coordinate is fixed.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Write a letter to the principal requesting him to grant class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Discuss the main reasons for poverty in India

10 examples of evaporation in daily life with explanations




