Question

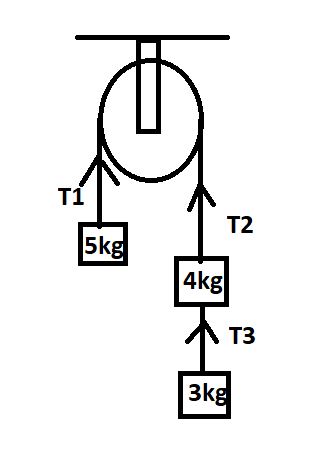
For the pulley mass system shown in figure, tension $ {T_3} $ in Newton is

(A) $ 25 $
(B) $ 30 $
(C) $ 35 $
(D) $ 40 $

Answer 1

Hint: Tension can be defined as the sum of forces on either end of the string or rope. If the two forces are pulling force then we need to add the two forces. In some cases, one force will not be a pulling force but works in the opposite direction. In that case we need to subtract this force from the other force pulling at the other hand. We will use the tension formula to solve this problem.

Complete Step By Step Answer:
Since the pulley is massless the tension $ {T_1} $ will be equal to $ {T_2} $ .
Mass of the first block $ {m_1} = 5kg $
Mass of the second block $ {m_2} = 4kg $
Mass of the third block $ {m_3} = 3kg $
The acceleration of the whole pulley system can be found using the following formula,
 $ \Rightarrow a = \dfrac{{{m_2}g + {m_3}g - {m_1}g}}{{{m_1} + {m_2} + {m_3}}} $
Substitute the values in the above equation,
 $ \Rightarrow a = \dfrac{{(4)g + (3)g - (5)g}}{{4 + 3 + 5}} $
Simplify the equation,
 $ \Rightarrow a = \dfrac{{2g}}{{12}} $
 $ \Rightarrow a = \dfrac{g}{6} $ …… (1)
For the third block, the tension formula can be written as,
 $ \Rightarrow mg - {T_3} = ma $
 $ \Rightarrow (3)g - {T_3} = (3)a $
Simplify the equation,
 $ \Rightarrow 3g - {T_3} = 3a $
Substituting equation (1) in the above equation,
 $ \Rightarrow 3g - {T_3} = 3 \times \dfrac{g}{6} $
 $ \Rightarrow 3g - {T_3} = \dfrac{g}{2} $
 $ \Rightarrow {T_3} = 3g - \dfrac{g}{2} $
Substituting for the gravitational acceleration, $ g = 10m/{s^2} $ we get,
 $ \Rightarrow {T_3} = 3(10) - \dfrac{{10}}{2} $
 $ \therefore {T_3} = 25N $
Therefore, the correct option is A.

Note:
The pulley function and rope together are used to transmit the force you exert, F it is also used to change the direction of that force.
In order to solve any problem that is based on the pulley system, the first step we need to understand is what are the given conditions and write down the constraints equations accordingly. Every time we need to assume three things they are:
The string that is used in the pulley system is taunted and inextensible
The string should be considered massless so that we can assume the tension to be uniform throughout.
The pulley used in the problem is massless.
The above assumptions can be used in almost all possible pulley systems. The pulley system should consist of fixed pulleys or movable pulleys.