
For ${x^2} + 2x + 5$ to be a factor of ${x^4} + p{x^2} + q$, the values of $p$ and $q$ must be, respectively.
A) $ - 2,5$
B) 5,25
C) 10,20
D) 6,25
E) 14,25
Answer
592.5k+ views
Hint: Divide the polynomial ${x^4} + p{x^2} + q$ with its factor ${x^2} + 2x + 5$ and find the remainder. If a polynomial is divided by its factor, then the remainder is equal to zero. Hence, equate the calculated remainder to zero and find the value of unknowns.
Complete step by step solution: Since, we are given that ${x^2} + 2x + 5$ be a factor of ${x^4} + p{x^2} + q$, then, if we will divide ${x^4} + p{x^2} + q$ by ${x^2} + 2x + 5$ , then the remainder will be zero.
A factor divides the number completely.
Hence, we will find the remainder after dividing ${x^4} + p{x^2} + q$ by ${x^2} + 2x + 5$ and equate that remainder to zero to find the value of unknowns.
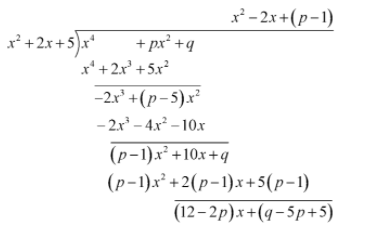
After, dividing we get the remainder as \[\left( {12 - 2p} \right)x + \left( {q - 5p + 5} \right)\]
Now, we will equate the remainder to be 0.
The coefficient of the $x$ should be 0 and the constant term of the remainder must be 0 for the complete remainder to be zero.
Equating the coefficient of $x$ to 0 and solve for the value of $p$
$
12 - 2p = 0 \\
\Rightarrow 2p = 12 \\
\Rightarrow p = 6 \\
$
Equating the constant term of the remainder to 0 , we get
\[q - 5p + 5 = 0\]
Substituting the value 6 for $p$ in the above equation and solve for the value of $q$
$
q - 5\left( 6 \right) + 5 = 0 \\
\Rightarrow q - 30 + 5 = 0 \\
\Rightarrow q = 25 \\
$
Thus option D is the correct answer.
Note: A polynomial is an algebraic expression is such as ${a_n}{x^n} + {a_{n - 1}}{x^{n - 1}} + ....{a_2}{x^2} + {a_1}x + {a_0}$,where \[n\] is the degree of polynomial when ${a_n} \ne 0$.When a polynomial is divided by its factor, then the remainder is zero. Also, the zeroes of the factor will be the zeroes of the polynomial. Divide the polynomial correctly to avoid incorrect answers.
Complete step by step solution: Since, we are given that ${x^2} + 2x + 5$ be a factor of ${x^4} + p{x^2} + q$, then, if we will divide ${x^4} + p{x^2} + q$ by ${x^2} + 2x + 5$ , then the remainder will be zero.
A factor divides the number completely.
Hence, we will find the remainder after dividing ${x^4} + p{x^2} + q$ by ${x^2} + 2x + 5$ and equate that remainder to zero to find the value of unknowns.
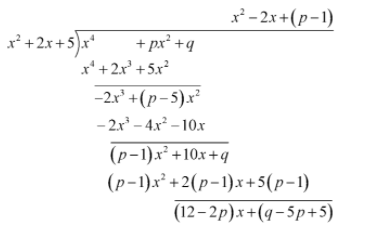
After, dividing we get the remainder as \[\left( {12 - 2p} \right)x + \left( {q - 5p + 5} \right)\]
Now, we will equate the remainder to be 0.
The coefficient of the $x$ should be 0 and the constant term of the remainder must be 0 for the complete remainder to be zero.
Equating the coefficient of $x$ to 0 and solve for the value of $p$
$
12 - 2p = 0 \\
\Rightarrow 2p = 12 \\
\Rightarrow p = 6 \\
$
Equating the constant term of the remainder to 0 , we get
\[q - 5p + 5 = 0\]
Substituting the value 6 for $p$ in the above equation and solve for the value of $q$
$
q - 5\left( 6 \right) + 5 = 0 \\
\Rightarrow q - 30 + 5 = 0 \\
\Rightarrow q = 25 \\
$
Thus option D is the correct answer.
Note: A polynomial is an algebraic expression is such as ${a_n}{x^n} + {a_{n - 1}}{x^{n - 1}} + ....{a_2}{x^2} + {a_1}x + {a_0}$,where \[n\] is the degree of polynomial when ${a_n} \ne 0$.When a polynomial is divided by its factor, then the remainder is zero. Also, the zeroes of the factor will be the zeroes of the polynomial. Divide the polynomial correctly to avoid incorrect answers.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Advantages and disadvantages of science

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What are the 12 elements of nature class 8 chemistry CBSE




