Question

Form the differential equation of the family of hyperbolas having foci on x-axis and centre at origin.

Answer 1

Hint: First, we will draw the diagram of hyperbola having a centre as origin and points of foci lies on x-axis. Then, there is formula which represent hyperbola having foci along x-axis is $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ . Also we have to do differentiation of this equation 2 times with respect to x because there are two variables in equation with the help of $\dfrac{d}{dx}{{x}^{n}}=n\cdot {{x}^{n-1}}$. If needed use quotient rule which is $\dfrac{d}{dx}\left[ \dfrac{f\left( x \right)}{g\left( x \right)} \right]=\dfrac{g\left( x \right)f'\left( x \right)-f\left( x \right)g'\left( x \right)}{{{\left( g\left( x \right) \right)}^{2}}}$ .

Complete step by step solution:
Now, we first write the formula which is used in this hyperbola family of two types. If foci points are situated along x-axis then equation is given as $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ and if foci points are along y-axis then the equation be slightly changed i.e. $\dfrac{{{y}^{2}}}{{{a}^{2}}}-\dfrac{{{x}^{2}}}{{{b}^{2}}}=1$ .
So, here we have foci points along the x-axis. Therefore, we will use $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ .

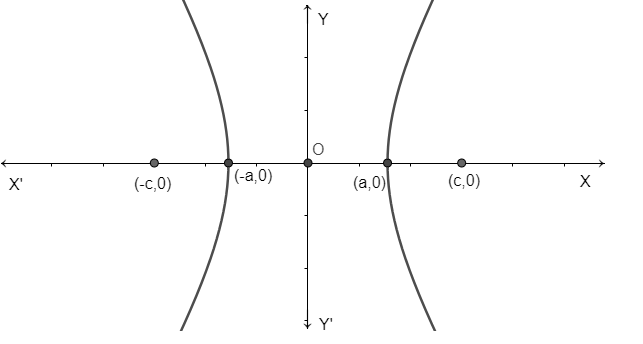
Now, we want to find differential equation of this family so, we have to do differentiation with respect to x 2 times as in equation there are 2 variables x and y by using the formula $\dfrac{d}{dx}{{x}^{n}}=n\cdot {{x}^{n-1}}$
So, differentiating both sides of the equation, we get
$\therefore \dfrac{d}{dx}\left[ \dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}} \right]=\dfrac{d}{dx}1$
$\therefore \dfrac{1}{{{a}^{2}}}\left( \dfrac{d}{dx}{{x}^{2}} \right)-\dfrac{1}{{{b}^{2}}}\left( \dfrac{d}{dx}{{y}^{2}} \right)=0$
Here, differentiation of any constant number will be zero and variable a, b are also constant so, taking out of the differentiation.
$\therefore \dfrac{1}{{{a}^{2}}}\left( 2\cdot {{x}^{2-1}} \right)-\dfrac{1}{{{b}^{2}}}\left( 2\cdot {{y}^{2-1}}\dfrac{dy}{dx} \right)=0$
$\therefore \dfrac{2}{{{a}^{2}}}\left( x \right)-\dfrac{2}{{{b}^{2}}}\left( y\cdot \dfrac{dy}{dx} \right)=0$
$\therefore \dfrac{2x}{{{a}^{2}}}-\dfrac{2}{{{b}^{2}}}\left( y\cdot \dfrac{dy}{dx} \right)=0$
Now, here variable y will not differentiate with respect to x. so, considering $\dfrac{dy}{dx}$ as $y'$ . And taking one term to right hand side, we get
$\therefore \dfrac{2x}{{{a}^{2}}}=\dfrac{2}{{{b}^{2}}}\left( yy' \right)$
On simplification, we get:
$\therefore \dfrac{x}{{{a}^{2}}}=\dfrac{y}{{{b}^{2}}}\left( y' \right)$
$\therefore \dfrac{{{b}^{2}}}{{{a}^{2}}}=\dfrac{yy'}{x}$ ……………………………………(i)
Here, using now quotient rule which is $\dfrac{d}{dx}\left[ \dfrac{f\left( x \right)}{g\left( x \right)} \right]=\dfrac{g\left( x \right)f'\left( x \right)-f\left( x \right)g'\left( x \right)}{{{\left( g\left( x \right) \right)}^{2}}}$ where \[f\left( x \right)=yy',g\left( x \right)=x\]. So, applying the rule in equation (i) we get,
$\dfrac{d}{dx}\left( \dfrac{{{b}^{2}}}{{{a}^{2}}} \right)=\dfrac{d}{dx}\left( \dfrac{yy'}{x} \right)$
 $0=\dfrac{x\cdot \left( yy' \right)'-\left( yy' \right)\dfrac{d}{dx}\left( x \right)}{{{x}^{2}}}$ (differentiation of constant term is zero)
On further simplification we get,
$x\cdot \left( yy' \right)'-\left( yy' \right)\left( 1 \right)=0\times {{x}^{2}}$
$x\cdot \left( yy' \right)'-\left( yy' \right)=0$ ……………………………….(ii)
Now here, the $2^{nd}$ term is independent of x so no need to differentiate further but in the first term there is x term so we will use the product rule on $\left( yy' \right)$ . Product rule is given by $\dfrac{d}{dx}f\left( x \right)g\left( x \right)=f\left( x \right)\dfrac{d}{dx}g\left( x \right)+g\left( x \right)\dfrac{d}{dx}f\left( x \right)$
Taking $f\left( x \right)=y,g\left( x \right)=y'$ , we get
$\therefore x\left[ \left( y\dfrac{d}{dx}y' \right)+\left( y'\dfrac{d}{dx}y \right) \right]=0$
 $\therefore x\left[ yy''+y'y' \right]=0$ ……………………………..(iii)
Now putting value of equation (iii) in equation (ii), we get
$\therefore x\left[ yy''+y'y' \right]-yy'=0$
$\therefore xyy''+xy{{'}^{2}}-yy'=0$ …………………………………..(iv)
Thus, the differential equation of the family of hyperbola is $xyy''+xy{{'}^{2}}-yy'=0$ .

Note: Be careful about what is asked in question because there are chances of making mistakes in ellipse and hyperbola general equation which is $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ and $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$. Also, all the rules of differentiation should be known when and where to apply properly. Make sure about differentiation answers as it becomes complex sometimes while solving. Also, while using quotient rule i.e. $\dfrac{d}{dx}\left[ \dfrac{f\left( x \right)}{g\left( x \right)} \right]=\dfrac{g\left( x \right)f'\left( x \right)-f\left( x \right)g'\left( x \right)}{{{\left( g\left( x \right) \right)}^{2}}}$ don’t consider $f\left( x \right)\cdot \dfrac{1}{g\left( x \right)}$ like this, otherwise the formula will become $\dfrac{d}{dx}\left[ \dfrac{f\left( x \right)}{g\left( x \right)} \right]=\dfrac{\dfrac{1}{g\left( x \right)}f'\left( x \right)-f\left( x \right)\dfrac{1}{g'\left( x \right)}}{{{\left( \dfrac{1}{g\left( x \right)} \right)}^{2}}}$ . So, it will be extremely complex and at last the result will be totally incorrect. So, please learn all the formulas which are needed to solve the problem.