Question

What is the formula for finding the area of an oval?

Answer 1

Hint: We know that ellipse is nothing but the shape of an elongated circle. First we will understand the basic shape of the ellipse and the terms longer radius and shorter radius associated with it. Hence we will write the formula for ellipse in terms of the two radii.

Complete step by step solution:
Now first let us understand the concept of oval.
Now the oval is nothing but the same as ellipse.
Ellipse is a two dimensional object. The shape looks like an elongated circle. Hence unlike a circle in ellipse we have the concept of minor radius and major radius.
Now the locus of the ellipse is nothing but all those points which have the sum of their distance is constant from two given fixed points on the axis. These two points are called foci of the ellipse.
Now an ellipse has two axis A major axis and minor axis. Both the axis of the ellipse passes through the center of the ellipse. Hence the largest diameter if the ellipse is called the major axis and the shortest diameter is called the minor axis.
Now let us check the equation of the ellipse. The equation of ellipse is given by \[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\].
Now let us check the figure of the ellipse or oval.

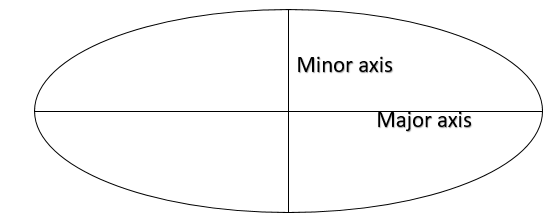
Now the area of the ellipse is given by $\pi \times a\times b$ where a is the longest radius and b is the smallest radius.
Consider the given figure of the oval shape.

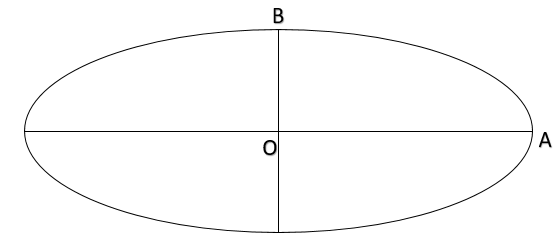
Here we can see that the longest radius is OB and the smallest radius is OA.
Hence we get the area of the given oval is given by $A=\pi \left( OA \right)\left( OB \right)$

Note: Now note that if the smallest radius and the largest radius of an ellipse are equal then the shapes we get is circle. Hence if we take the common radius to be r we get the formula for the area of the circle which is $\pi {{r}^{2}}$.