Question

What is the formula for the speed of a pendulum at any point?

Answer 1

Hint: To calculate the speed of the pendulum at any point in space, we will consider the pendulum to be a simple pendulum with very small oscillations. This approximation will help us derive the formula for Force on the pendulum bob at any instant as a function of acceleration which can then be used to get the speed of the pendulum.

Complete step-by-step solution:
Let us assume that the bob of the pendulum has a mass ‘m’. The length of the string, that is, the length of the pendulum is ‘l’ and the gravitational acceleration is ‘g’. Then, for very small oscillation, we can say that:
$\Rightarrow \sin \theta \approx \theta $
Now, let us see the different types of forces acting on the pendulum bob when it is set in motion with the help of the following diagram:

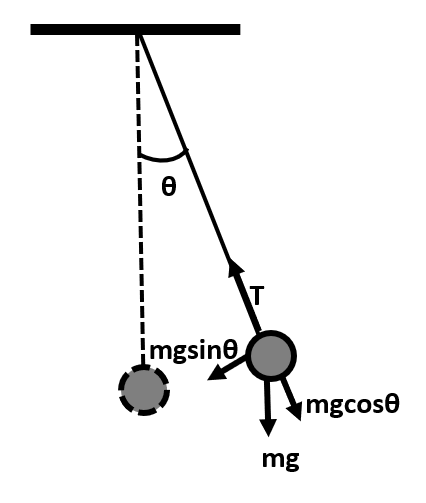
Here, we can see that the perpendicular component of mg, that is, $mg\sin \theta $ is the restoring force on the pendulum.
Thus, using Newton’s second law of motion, the linear acceleration (a) of the pendulum can be written as:
$\Rightarrow a=-g\sin \theta $ [Let this expression be equation number (1)]
Also, since the bob is moving along the arc of the circle, its angular acceleration is given by:
$\Rightarrow \alpha =\dfrac{{{d}^{2}}\theta }{d{{t}^{2}}}$ [Let this expression be equation number (2)]
Which can also be written as:
$\Rightarrow \alpha =\dfrac{a}{l}$ [Let this expression be equation number (3)]
Thus, from equation number (1), (2) and (3), we have:
$\Rightarrow \dfrac{{{d}^{2}}\theta }{d{{t}^{2}}}=-\dfrac{g}{l}\sin \theta $
Using the approximation from earlier, we have:
$\begin{align}
  & \Rightarrow \dfrac{{{d}^{2}}\theta }{d{{t}^{2}}}=-\dfrac{g}{l}\theta \\
 & \Rightarrow m\dfrac{{{d}^{2}}\theta }{d{{t}^{2}}}=-m\dfrac{g}{l}\theta \\
 & \Rightarrow F=-kx \\
\end{align}$
Where, F is the net restoring force and ‘k’ is a constant equal to $\dfrac{mg}{l}$ .
Thus, the pendulum is exhibiting a simple harmonic motion. Thus, the speed of the pendulum can be written using the equation of speed of a particle exhibiting S.H.M. . This is done as follows:
$\Rightarrow v=A\omega \cos (\omega t+\phi )$
Where,
A is the amplitude of oscillatory motion.
‘$\omega $’ is the angular frequency of the motion which is equal to:
$\begin{align}
  & \Rightarrow \omega =\sqrt{\dfrac{k}{m}} \\
 & \Rightarrow \omega =\sqrt{\dfrac{\dfrac{mg}{l}}{m}} \\
 & \therefore \omega =\sqrt{\dfrac{g}{l}} \\
\end{align}$
And, $\phi $ is the initial phase of the particle.
Hence, the formula for speed of the pendulum at any point comes out to be $A\omega \cos (\omega t+\phi )$.

Note: We should always know the derivation of these crucial terms such as the velocity and displacement of a particle in S.H.M. and also know the assumptions under which these formulas have been derived as changing those assumptions will give us different set of equations than desired ones.