Question

What is the formula of area of triangle in coordinate geometry?

Answer 1

Hint: Here, in this problem, we need to understand the concept of coordinate geometry and area of triangle. After that we need to derive the formula of area of triangle in coordinate geometry by drawing the figure and to find the area of triangle, we need to use the tree vertices in coordinate geometry.

Complete step-by-step solution:
Before solving the problem, we need to understand the concept of coordinate geometry that is,
Coordinate geometry is defined as the study of geometry using coordinate points. The area of a triangle in coordinate geometry can be calculated if the three vertices of the triangle are given in the coordinate plane.
In coordinate geometry, if we need to find the area of a triangle, we use the coordinates of the three vertices. For better understanding the problem figure is given below:

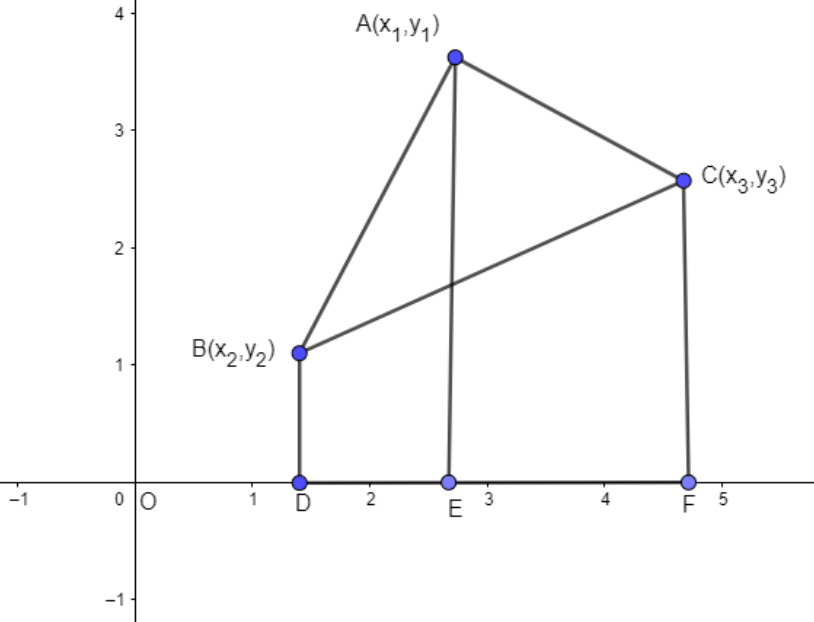
Consider $$\mathrm{\Delta }ABC$$ as given in the figure below with vertices $$A(x_1,y_1)$$, $$B(x_2,y_2)$$ and $$C(x_3,y_3)$$.
In this figure, we have drawn perpendiculars AE, CF, and BD from the vertices of the triangle to the horizontal axis. Notice that three trapeziums are formed: BAED, ACFE, and BCFD.
We can express the area of a triangle in terms of the areas of these three trapeziums.
$$Area\left(\mathrm{\Delta }ABC\right)=Area(Trap.BAED)+Area(Trap.ACFE)-Area(Trap.BCFD)$$
Now, the area of a trapezium in terms of the lengths of the parallel sides (the bases of the trapezium) and the distance between the parallel sides (the height of the trapezium):
$$\Rightarrow \text{Trapezium}\text{Area}=\left({\displaystyle \frac{1}{2}}\right)\times \left(\text{Sum}\text{of}\text{bases}\right)\times \text{Height}$$
Consider any one trapezium, say BAED. Its bases are BD and AE, and its height is DE.
$$\Rightarrow Area(Trap.BAED)=\left({\displaystyle \frac{1}{2}}\right)\times (BD+AE)\times \left(DE\right)$$
BD and AE can easily be seen to be the y coordinates of B and A, while DE is the difference between the x coordinates of A and B. Similarly, the bases and heights of the other two trapeziums can be easily calculated. Thus, we have;
$$\Rightarrow Area(Trap.BAED)=\left({\displaystyle \frac{1}{2}}\right)\times (y_1+y_2)\times (x_1-x_2)---(1)$$
Similarly, we can also find the Area of trapezium ACFE.
$$\Rightarrow Area(Trap.ACFE)=\left({\displaystyle \frac{1}{2}}\right)\times (AE+CF)\times \left(EF\right)$$
By substituting the values, we get:
$$\Rightarrow Area(Trap.ACFE)=\left({\displaystyle \frac{1}{2}}\right)\times (y_1+y_3)\times (x_1-x_3)---(2)$$
Area of Trapezium BCFD is given by
$$\Rightarrow Area(Trap.BCFD)=\left({\displaystyle \frac{1}{2}}\right)\times (BD+CF)\times \left(DF\right)$$
By substituting the values, we get:
 $$\Rightarrow Area(Trap.BCFD)=\left({\displaystyle \frac{1}{2}}\right)\times (y_2+y_3)\times (x_3-x_2)---(3)$$
The expression for the area of the triangle in terms of the coordinates of its vertices can thus be given as,
$$Area\left(\mathrm{\Delta }ABC\right)=Area(Trap.BAED)+Area(Trap.ACFE)-Area(Trap.BCFD)--(4)$$
By substituting the value of equation (1), (2) and (3) on equation (4) we get:
$$Area\left(\mathrm{\Delta }ABC\right)=\left({\displaystyle \frac{1}{2}}\right)\times (y_1+y_2)\times (x_1-x_2)+\left({\displaystyle \frac{1}{2}}\right)\times (y_1+y_3)\times (x_1-x_3)-\left({\displaystyle \frac{1}{2}}\right)\times (y_2+y_3)\times (x_3-x_2)$$
However, we should try to simplify it so that it is easy to remember.
For that, we simplify the product of the two brackets in each term:
Take the common term $${\displaystyle \frac{1}{2}}$$ outside the bracket we get:
$$Area\left(\mathrm{\Delta }ABC\right)=\left({\displaystyle \frac{1}{2}}\right)\times [x_1{y}_2-x_2{y}_2+x_1{y}_1-x_2{y}_1-x_3{y}_1+x_1{y}_1-x_3{y}_3+x_1{y}_3+x_3{y}_2+x_2{y}_2-x_3{y}_3+x_2{y}_3]$$
By simplifying this further we get:
$$Area\left(\mathrm{\Delta }ABC\right)=\left({\displaystyle \frac{1}{2}}\right)\times [x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]$$
As the area is always positive,
$$Area\left(\mathrm{\Delta }ABC\right)=\left({\displaystyle \frac{1}{2}}\right)\times |x_1(y_2-y_3)+x_2(y_3-y_2)+x_3(y_1-y_2)|$$
This is a symmetric expression,
Hence, this is an Area of triangle in coordinate geometry is $$\left({\displaystyle \frac{1}{2}}\right)\times |x_1(y_2-y_3)+x_2(y_3-y_2)+x_3(y_1-y_2)|$$.

Note: The area of a triangle cannot be negative. In case we get the answer in negative terms, we should consider the numerical value of the area, without the negative sign. To find the area of a triangle in coordinate geometry, we need to find the length of three sides of a triangle using the distance formula. there is an easy technique to remember it, by using the determinant form that is which is given by Area $$=\left({\displaystyle \frac{1}{2}}\right)\times \left|\begin{array}{ccc}{x}_1& y_1& 1\\ x_2& y_2& 1\\ x_3& y_3& 1\end{array}\right|$$. This formula we generally use to find the area of a triangle in coordinate geometry.