Question

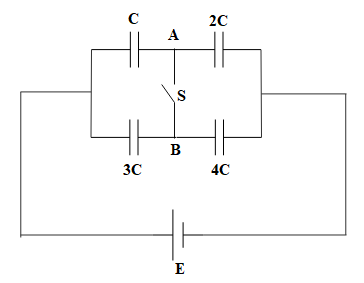
Four capacitors of capacitances $C,2C,3C\text{ and }4C$ are connected as shown. At $t=0,$ S is closed. Find the charge flowing through connector AB.
A.$\dfrac{CE}{5}$
B.$\dfrac{CE}{3}$
C.$\dfrac{CE}{2}$
D.$\dfrac{CE}{6}$

Answer 1

Hint: We shall first analyze the two situations separately when the switch is closed and when it is open. Then we will find the total capacitance of the arrangement shown and simultaneously the charge associated with it. Further, according to the polarity of the plates of the capacitors, the charge in connector AB will be calculated.

Complete answer:
The charge $\left( Q \right)$, voltage $\left( V \right)$ and capacitance of the capacitor are related as:
$Q=CV$ ……………. Equation (1)
Initially when S is closed, the circuit is as follows:

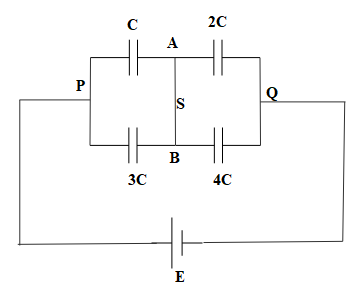
The capacitors with capacitances C and 2C are in series with each other and their resultant capacitance, ${{C}_{e{{q}_{1}}}}$ is given as:
$\begin{align}
  & \dfrac{1}{{{C}_{e{{q}_{1}}}}}=\dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{2}}} \\
 & \Rightarrow \dfrac{1}{{{C}_{e{{q}_{1}}}}}=\dfrac{1}{C}+\dfrac{1}{2C} \\
 & \Rightarrow \dfrac{1}{{{C}_{e{{q}_{1}}}}}=\dfrac{2C+C}{\left( 2C \right)\left( C \right)} \\
\end{align}$
$\begin{align}
  & \Rightarrow {{C}_{e{{q}_{1}}}}=\dfrac{\left( 2C \right)\left( C \right)}{3C} \\
 & \Rightarrow {{C}_{e{{q}_{1}}}}=\dfrac{2C}{3} \\
\end{align}$
Using equation (1),
Charge in this upper branch is, ${{Q}_{1}}=CV$
$\Rightarrow {{Q}_{1}}=\left( \dfrac{2C}{3} \right)E$
$\therefore {{Q}_{1}}=\dfrac{2CE}{3}$
Also, the capacitors with capacitances 3C and 4C are in series with each other and their resultant capacitance, ${{C}_{e{{q}_{2}}}}$ is given as:
$\begin{align}
  & \dfrac{1}{{{C}_{e{{q}_{2}}}}}=\dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{2}}} \\
 & \Rightarrow \dfrac{1}{{{C}_{e{{q}_{2}}}}}=\dfrac{1}{3C}+\dfrac{1}{4C} \\
 & \Rightarrow \dfrac{1}{{{C}_{e{{q}_{2}}}}}=\dfrac{4C+3C}{\left( 3C \right)\left( 4C \right)} \\
\end{align}$
$\begin{align}
  & \Rightarrow {{C}_{e{{q}_{2}}}}=\dfrac{\left( 3C \right)\left( 4C \right)}{7C} \\
 & \Rightarrow {{C}_{e{{q}_{2}}}}=\dfrac{12C}{7} \\
\end{align}$
Using equation (1),
Charge in this upper branch is, ${{Q}_{2}}=CV$
$\Rightarrow {{Q}_{2}}=\left( \dfrac{12C}{7} \right)E$
$\therefore {{Q}_{2}}=\dfrac{12CE}{7}$
We shall now analyze the charges on the plates of the capacitors. They are as depicted in the diagram:

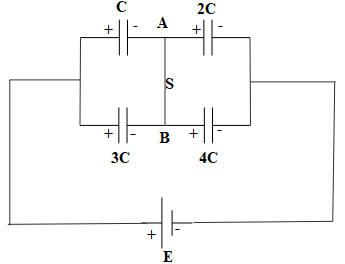
When S is closed, capacitors C and 3C are connected in parallel,
Their equivalent capacitance is given as:
${{C}_{eq}}=C+3C$
\[\Rightarrow {{C}_{eq}}^{1}=4C\]
Also, capacitors 2C and 4C are connected in parallel,
Their equivalent capacitance is given as:
${{C}_{eq}}=2C+4C$
\[\Rightarrow {{C}_{eq}}^{2}=6C\]
The circuit is now transformed as:

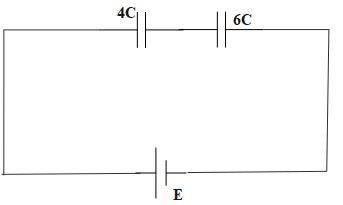
Thus, the total capacitance is:
$\begin{align}
  & \dfrac{1}{{{C}_{eq}}}=\dfrac{1}{{{C}_{eq}}^{1}}+\dfrac{1}{{{C}_{eq}}^{2}} \\
 & \Rightarrow \dfrac{1}{{{C}_{eq}}}=\dfrac{1}{4C}+\dfrac{1}{6C} \\
 & \Rightarrow \dfrac{1}{{{C}_{eq}}}=\dfrac{6C+4C}{\left( 4C \right)\left( 6C \right)} \\
\end{align}$
$\begin{align}
  & \Rightarrow {{C}_{eq}}=\dfrac{\left( 4C \right)\left( 6C \right)}{10C} \\
 & \Rightarrow {{C}_{eq}}=\dfrac{24C}{10} \\
\end{align}$
$\therefore {{C}_{eq}}=2.4C$
Using equation (1), the total charge is $Q=2.4C\left( E \right)$
Since 4C and 6C capacitors were in series, therefore both of them acquire charge $2.4CE$respectively.
However, 4C capacitance consists of capacitors C and 3C in parallel.
$\Rightarrow {{Q}_{C}}+{{Q}_{3C}}=2.4CE$ ……………………. Equation (2)

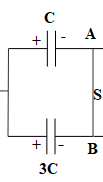
Therefore, ${{V}_{C}}={{V}_{3C}}$,
$\begin{align}
  & \Rightarrow \dfrac{C}{{{Q}_{C}}}=\dfrac{3C}{{{Q}_{3C}}} \\
 & \Rightarrow {{Q}_{3C}}=3{{Q}_{C}} \\
\end{align}$
Combining equation (2) with this, we get
$\begin{align}
  & \Rightarrow {{Q}_{C}}+3{{Q}_{C}}=2.4CE \\
 & \Rightarrow 4{{Q}_{C}}=2.4CE \\
 & \Rightarrow {{Q}_{C}}=0.6CE \\
\end{align}$
Similarly, 6C capacitance consists of 2C and 4C,
$\Rightarrow {{Q}_{2C}}+{{Q}_{4C}}=2.4CE$ ……………………. Equation (3)

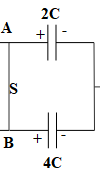
Therefore, ${{V}_{2C}}={{V}_{4C}}$,
$\begin{align}
  & \Rightarrow \dfrac{2C}{{{Q}_{2C}}}=\dfrac{4C}{{{Q}_{4C}}} \\
 & \Rightarrow {{Q}_{4C}}=2{{Q}_{2C}} \\
\end{align}$
Combining equation (2) with this, we get
$\begin{align}
  & \Rightarrow {{Q}_{2C}}+2{{Q}_{2C}}=2.4CE \\
 & \Rightarrow 3{{Q}_{2C}}=2.4CE \\
 & \Rightarrow {{Q}_{2C}}=0.8CE \\
\end{align}$
The charge at junction A is $-{{Q}_{C}}+{{Q}_{2C}}=-0.6CE+0.8CE=0.2CE$
Thus, the charge in connector AB is $0.2CE=\dfrac{2CE}{10}=\dfrac{CE}{5}$

Therefore, the correct option is (A) $\dfrac{CE}{5}$

Note:
Capacitors C and 3C are connected with the positive terminal of the battery, therefore, their left plate will acquire a positive charge and their right plate will acquire negative charge. Likewise, capacitors 2C and 4C are connected with the negative terminal of the battery, therefore, their right plate will acquire negative charge and their left plate will acquire positive charge.