Question

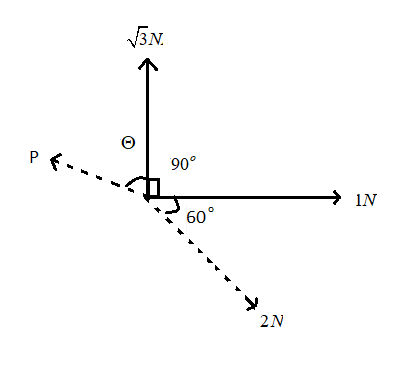
Four coplanar concurrent forces are acting on a body as shown in the figure to keep it in equilibrium. Then the value of $P$ and $\Theta $ are

                                  

A. $P = 4N,\Theta = {90^o}$
B. $P = 2N,\Theta = {90^o}$
C. $P = 1N,\Theta = {90^o}$
D. $P = 5N,\Theta = {90^o}$

Answer 1

Hint: We know that the coplanar concurrent forces is the system of two or more forces acting on the same plane intersecting the same point on the plane. This problem is solved by the coplanar concurrent forces system. When all the forces are acting in the same plane, they are known as coplanar forces whereas when the forces act at the same point on the same plane at same time, it is known as concurrent forces.

Complete answer:
We can split each force in two or more components , this is known as resolution of a force. After the resolution of the force the effect of the force remains as it is as earlier. So we can split up the force in two perpendicular components i.e. horizontal components and vertical components.

The resultant of concurrent forces can be found by resolving each force into its rectangular components. After that we add the all components algebraically according to their direction such as all the components along the y-axis are added together and along the x-axis are added together and sum of all the forces is zero :\[{F_X} = 0,{F_Y} = 0\].

For the given question , balancing the forces in the y-direction,
$
  \sqrt 3 + p\cos \theta - 2 \times \sin {60^0} = 0 \\
  \Rightarrow \sqrt 3 + p\cos \theta - 2 \times \dfrac{{\sqrt 3 }}{2} = 0 \\
   \Rightarrow p\cos \theta = 0 \\
$

So the, $\theta = {90^0}$
For balancing the force along the X-direction, $1 + 2 \times \dfrac{1}{2} - p \times 1 = 0$$ \Rightarrow p = 2$.

So, the correct answer is “Option B”.

Note:
If all the forces acting on the body, keeps the body in the resting state or in the uniform motion in which its velocity is constant, then the system is said to be in equilibrium and net force on the system is zero in that condition.