
Four point charges, each of $+q$, are rigidly fixed at the four corners of a square planar soap film of side ‘a’. the surface tension of the soap film is $\gamma $. The system of charges and planar film are in equilibrium, and $a=k{{\left[ \dfrac{{{q}^{2}}}{\gamma } \right]}^{\dfrac{1}{N}}}$, where ‘k’ is a constant. Then N is:
A. 3
B. 2
C. 4
D. 9
Answer
582.9k+ views
Hint: To solve this question, first find the force acting in any one of the charges in the corner of the square soap film. Then find the force on the soap film due to its surface film. Since the system of charges and the planar film is in equilibrium, we will equate the two forces and then we can find our answer.
Complete answer:
There are four charges at the corners of a square.
The side of the square is a.
Let us draw a diagram of the system given in the question.
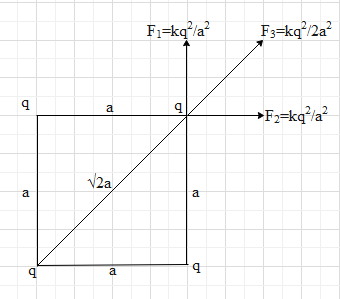
Now, the force in any of the charges due to one of the neighbouring charges,
${{F}_{1}}={{F}_{2}}=\dfrac{k{{q}^{2}}}{{{a}^{2}}}$
Now, the force on any charge due to the charge in the diagonal position is,
${{F}_{3}}=\dfrac{k{{q}^{2}}}{{{\left( \sqrt{2}a \right)}^{2}}}$
So, the net force on any of the charges in the corner of the square is,
$\begin{align}
& F={{F}_{3}}+\sqrt{\left( {{F}_{1}}^{2}+{{F}_{2}}^{2} \right)} \\
& F=\dfrac{k{{q}^{2}}}{2{{a}^{2}}}+\sqrt{2}\dfrac{k{{q}^{2}}}{{{a}^{2}}} \\
& F=\dfrac{{{q}^{2}}}{{{a}^{2}}}\times \text{constant}\text{.} \\
\end{align}$
The force on the side due to the surface tension on the soap film can be mathematically expressed as,
$\begin{align}
& F=\text{ surface tension }\times \text{ side length} \\
& \text{F=}\gamma \text{a} \\
\end{align}$
Since the system as a whole is in equilibrium, the outward force due to forces of the charges and the inward force due to the surface tension of the soap film will be equal.
Equating the two forces,
$\begin{align}
& \dfrac{{{q}^{2}}}{{{a}^{2}}}\times \text{constant=}\gamma \text{a} \\
& {{a}^{3}}=\dfrac{{{q}^{2}}}{\gamma }\times \text{constant} \\
& a\text{=}{{\left[ \dfrac{{{q}^{2}}}{\gamma }\times \text{constant} \right]}^{\dfrac{1}{3}}} \\
& a=K{{\left[ \dfrac{{{q}^{2}}}{\gamma } \right]}^{\dfrac{1}{3}}} \\
\end{align}$
Now, given in the question that the expression for the side length of the square is,
$a=k{{\left[ \dfrac{{{q}^{2}}}{\gamma } \right]}^{\dfrac{1}{N}}}$
Comparing the above two expression we get that,
$\begin{align}
& \dfrac{1}{3}=\dfrac{1}{N} \\
& N=3 \\
\end{align}$
So, the value of N will be 3.
The correct option is (A).
Note:
Surface tension is the tendency of liquid surfaces to shrink into the minimum surface area. So, the surface tension exerts an inward force in the liquid surface. Force due to surface tension depends on the value of surface tension and the side length or the perimeter of the liquid surface.
Complete answer:
There are four charges at the corners of a square.
The side of the square is a.
Let us draw a diagram of the system given in the question.
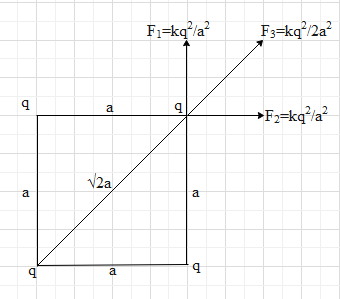
Now, the force in any of the charges due to one of the neighbouring charges,
${{F}_{1}}={{F}_{2}}=\dfrac{k{{q}^{2}}}{{{a}^{2}}}$
Now, the force on any charge due to the charge in the diagonal position is,
${{F}_{3}}=\dfrac{k{{q}^{2}}}{{{\left( \sqrt{2}a \right)}^{2}}}$
So, the net force on any of the charges in the corner of the square is,
$\begin{align}
& F={{F}_{3}}+\sqrt{\left( {{F}_{1}}^{2}+{{F}_{2}}^{2} \right)} \\
& F=\dfrac{k{{q}^{2}}}{2{{a}^{2}}}+\sqrt{2}\dfrac{k{{q}^{2}}}{{{a}^{2}}} \\
& F=\dfrac{{{q}^{2}}}{{{a}^{2}}}\times \text{constant}\text{.} \\
\end{align}$
The force on the side due to the surface tension on the soap film can be mathematically expressed as,
$\begin{align}
& F=\text{ surface tension }\times \text{ side length} \\
& \text{F=}\gamma \text{a} \\
\end{align}$
Since the system as a whole is in equilibrium, the outward force due to forces of the charges and the inward force due to the surface tension of the soap film will be equal.
Equating the two forces,
$\begin{align}
& \dfrac{{{q}^{2}}}{{{a}^{2}}}\times \text{constant=}\gamma \text{a} \\
& {{a}^{3}}=\dfrac{{{q}^{2}}}{\gamma }\times \text{constant} \\
& a\text{=}{{\left[ \dfrac{{{q}^{2}}}{\gamma }\times \text{constant} \right]}^{\dfrac{1}{3}}} \\
& a=K{{\left[ \dfrac{{{q}^{2}}}{\gamma } \right]}^{\dfrac{1}{3}}} \\
\end{align}$
Now, given in the question that the expression for the side length of the square is,
$a=k{{\left[ \dfrac{{{q}^{2}}}{\gamma } \right]}^{\dfrac{1}{N}}}$
Comparing the above two expression we get that,
$\begin{align}
& \dfrac{1}{3}=\dfrac{1}{N} \\
& N=3 \\
\end{align}$
So, the value of N will be 3.
The correct option is (A).
Note:
Surface tension is the tendency of liquid surfaces to shrink into the minimum surface area. So, the surface tension exerts an inward force in the liquid surface. Force due to surface tension depends on the value of surface tension and the side length or the perimeter of the liquid surface.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




