Question

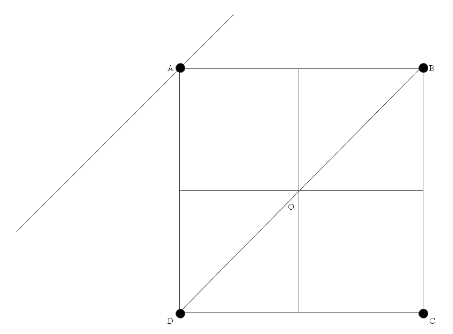
Four point masses each of value $m$, are placed at the corners of a square ABCD of side $l$. The moment of inertia of this system about an axis through A and parallel to BD is

A) $m{l^2}$
B) $2m{l^2}$
C) $\sqrt 3 m{l^2}$
D) $3m{l^2}$

Answer 1

Hint: A point mass only contributes to the moment of inertia when the axis of rotation does not pass through it. Calculate the distance of each point mass from the axis of rotation and use the formula for calculating the moment of inertia of a system of particles.

Formula used: The moment of inertia of a system of particles is given as:
$\Rightarrow I = \sum\limits_{i = 1}^n {{m_i}{r_i}^2} $where $I$ is the moment of inertia, ${m_i}$ and ${r_i}$ are the mass and distance of the ith point mass from the axis of rotation.

Complete step by step solution:
Before finding the moment of inertia, we need to find the perpendicular distance of all the point masses from the axis of rotation. Since the axis passes through the point mass at point A, it won’t contribute to the moment of inertia of the system.
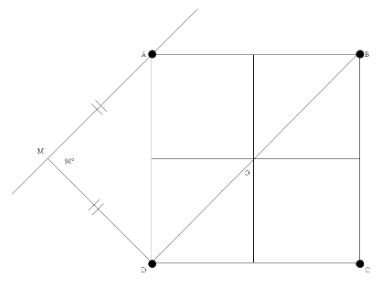
From the geometry shown in the image below, we know that $AM = MD$ and from Pythagoras theorem, we have $A{M^2} + M{D^2} = A{D^2}$ so we can obtain:
$2M{D^2} = A{D^2}$
Substituting the length of $AD = l$, we get:
$\Rightarrow 2M{D^2} = {l^2}$
$\Rightarrow M{D^2} = \dfrac{{{l^2}}}{2}$
Taking the square root on both sides, we get:
$\Rightarrow MD = \dfrac{l}{{\sqrt 2 }}$

Hence, the perpendicular distance of point D from the axis of rotation is $\dfrac{l}{{\sqrt 2 }}$. Similarly, the distance of B from the axis of rotation will also be equal to $\dfrac{l}{{\sqrt 2 }}$.
The perpendicular distance of C from the axis of rotation is equal to the length of the diagonal of the square which we know is $\sqrt 2 l$.
Now that we know all the perpendicular distances of the point masses from the axis of rotation, we can use the formula to find the moment of inertia as:
$\Rightarrow I = m{\left( {\dfrac{l}{{\sqrt 2 }}} \right)^2} + m{\left( {\sqrt 2 l} \right)^2} + m{\left( {\dfrac{l}{{\sqrt 2 }}} \right)^2}$
$\Rightarrow I = \dfrac{{m{l^2}}}{2} + 2m{l^2} + \dfrac{{m{l^2}}}{2}$
On adding all the individual moments of inertia, we obtain the total moment of inertia of the system as:
$\therefore I = 3m{l^2}$
Hence, the moment of inertia of this system about an axis through A and parallel to BD is $3m{l^2}$.

Note:
While calculating the moment of inertia, we must be careful to not count the point mass A since the axis of rotation passes from it. Familiarity with square geometry and the Pythagoras theorem can make the task of finding distances of the points from the axis of rotation very simple.