Question

Four resistors A, B, C, and D form a Wheatstone bridge. The bridge is balanced when C = $100\Omega $. If A and B are interchanged, the bridge balances for $C = 121\Omega $. The value of D is:
A. $10\Omega $
B. $100\Omega $
C. $110\Omega $
D. $120\Omega $

Answer 1

Hint: It is important to understand the balance condition for a Wheatstone’s bridge in order to go ahead with this problem. The Wheatstone’s network is said to be balanced when there is no current flowing in the galvanometer.

Complete Step by Step Answer:
Consider the following network of four resistors A, B, C, and D as arranged in the Wheatstone’s bridge with G as the galvanometer.

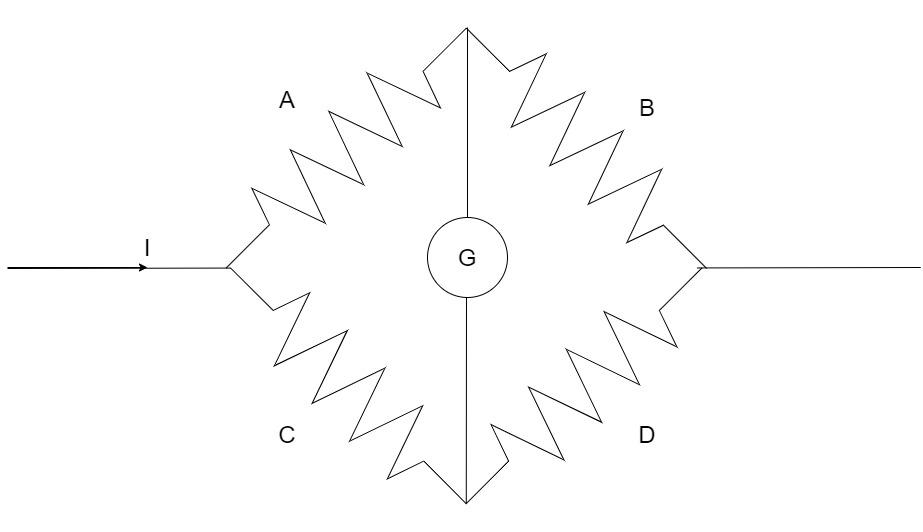
The galvanometer is said to be balanced if there is no current flowing through the galvanometer G in the figure. This can be achieved by having the 4 resistances in the following ratio:
$\dfrac{A}{B} = \dfrac{C}{D}$
In the question, it is given that the bridge is balanced when $C = 100\Omega $
Substituting, we have
$ \dfrac{A}{B} = \dfrac{{100}}{D} $
Rearranging the terms,
$\Rightarrow D = \dfrac{{100B}}{A}$
Now, in the question, he says that by interchanging the resistance B and A, we are getting a new value of bridge balance condition for C i.e. $C = 121\Omega $.
Thus, the new bridge balance equation becomes:
$\Rightarrow \dfrac{B}{A} = \dfrac{C}{D}$
Substituting the new value of C in the above equation, we get –
$\Rightarrow \dfrac{B}{A} = \dfrac{{121}}{D}$
Since the values of these individual resistances have not been changed, the value of $B/A$ can be substituted in the above equation for D.
$\Rightarrow D = \dfrac{{100B}}{A}$
Substituting,
$ D = 100 \times \dfrac{B}{A} \\
  D = 100 \times \dfrac{{121}}{D} \\
 $
Rearranging the terms, we get –
$\Rightarrow {D^2} = 100 \times 121$
Tip: Instead of multiplying the RHS and taking the square root, we can directly apply the square root since both the numbers 100 and 121 are perfect squares.
$
  \Rightarrow D = \sqrt {100 \times 121} \\
  D = \sqrt {\underline {10} \times 10 \times \underline {11} \times 11} = 10 \times 11 = 110\Omega \\
 $
$\therefore$ The value of Resistor D is $110\Omega $. Hence, option (C) is the correct answer.

Note:
The order of the resistances in the Wheatstone’s network should be exactly in the same order or it will result in a wrong bridge condition. Hence, we cannot byheart the bridge balance condition and get confused when the question is twisted. Hence, I will give you a shortcut method to remember the bridge balance condition.
Consider the circuit diagram :

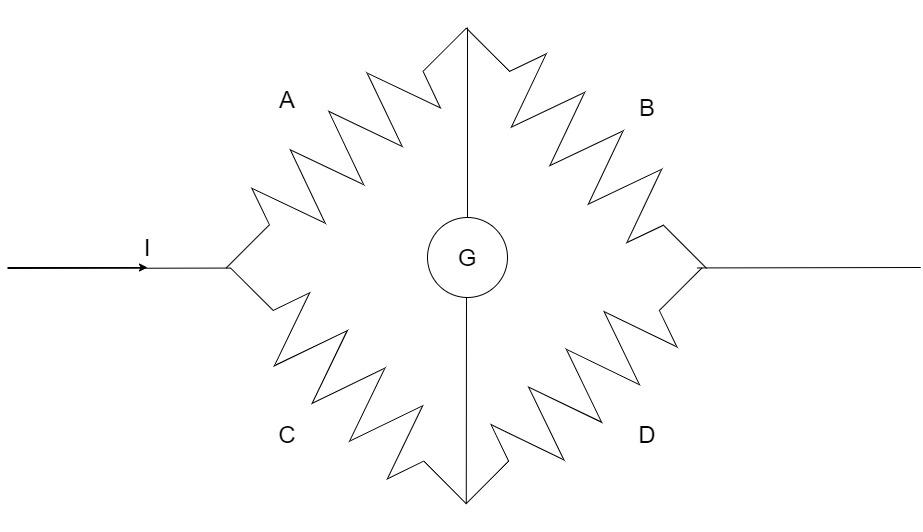
The bridge balance condition is :
$\dfrac{{Left}}{{Right}} = \dfrac{{Left}}{{Right}}$
We can see that the numerators have the resistances on the left of the galvanometer and the denominators have the resistances right of the galvanometer. Note that the left and right here refer to the relative position of the resistances with the galvanometer, so look carefully, if the Wheatstone’s network is inverted or given in any other configuration.